目標

在本教程中，您將學習如何

什麼是支援向量機（SVM）？

支援向量機（SVM）是一種判別分類器，其正式定義為一個分離超平面。換句話說，給定有標籤的訓練資料（監督學習），該演算法會輸出一個最優超平面，用於對新樣本進行分類。

所獲得的超平面在何種意義上是“最優”的？讓我們考慮以下簡單問題：

對於一個線性可分的二維點集，這些點屬於兩個類別之一，請找到一條分離直線。

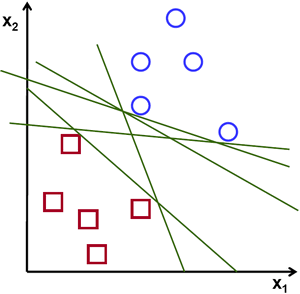
注意: 在這個例子中，我們處理的是笛卡爾平面中的直線和點，而不是高維空間中的超平面和向量。這是一個簡化的問題。重要的是要理解，這樣做只是因為我們更容易從易於想象的例子中建立直觀認識。然而，相同的概念也適用於分類任務，其中待分類的樣本位於維度高於二的空間中。

在上圖中，您可以看到存在多條直線可以解決該問題。其中是否有哪一條比其他的更好？我們可以憑直覺定義一個標準來評估直線的價值：如果一條直線過於靠近點，則它不好，因為它對噪聲敏感，並且無法正確泛化。因此，我們的目標應該是找到一條儘可能遠離所有點的直線。

因此，SVM演算法的操作基於找到一個超平面，該超平面能提供到訓練樣本的最大最小距離。這個距離的兩倍在SVM理論中被賦予了重要的名稱：間隔（margin）。因此，最優分離超平面會最大化訓練資料的間隔。

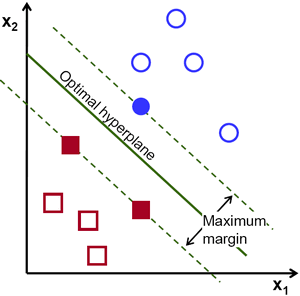
讓我們引入用於正式定義超平面的符號：

\[f(x) = \beta_{0} + \beta^{T} x,\]

其中 \(\beta\) 被稱為權重向量，\(\beta_{0}\) 被稱為偏置。

注意: 關於這一點和超平面的更深入描述，您可以在T. Hastie、R. Tibshirani和J. H. Friedman所著的《統計學習的要素》（Elements of Statistical Learning）一書的4.5節（分離超平面）中找到 ([276])。

透過對 \(\beta\) 和 \(\beta_{0}\) 進行縮放，最優超平面可以用無數種不同的方式表示。按照慣例，在所有可能的超平面表示中，選擇的是：

\[|\beta_{0} + \beta^{T} x| = 1\]

其中 \(x\) 象徵著離超平面最近的訓練樣本。通常，離超平面最近的訓練樣本被稱為支援向量（support vectors）。這種表示方式被稱為規範超平面（canonical hyperplane）。

現在，我們使用幾何學中關於點 \(x\) 與超平面 \((\beta, \beta_{0})\) 之間距離的結果：

\[\mathrm{distance} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||}.\]

特別是對於規範超平面，分子等於1，到支援向量的距離為：

\[\mathrm{distance}_{\text{ support vectors}} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||} = \frac{1}{||\beta||}.\]

回想一下前一節中引入的間隔，這裡表示為 \(M\)，它是到最近樣本距離的兩倍：

\[M = \frac{2}{||\beta||}\]

最後，最大化 \(M\) 的問題等價於在某些約束條件下最小化函式 \(L(\beta)\) 的問題。這些約束條件模擬了超平面正確分類所有訓練樣本 \(x_{i}\) 的要求。形式上：

\[\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \text{ 滿足 } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \text{ } \forall i,\]

其中 \(y_{i}\) 代表每個訓練樣本的標籤。

這是一個拉格朗日最佳化問題，可以透過使用拉格朗日乘數來求解，以獲得最優超平面的權重向量 \(\beta\) 和偏置 \(\beta_{0}\)。

本練習的訓練資料由一組帶有標籤的二維點組成，它們屬於兩個不同類別中的一個；其中一個類別包含一個點，另一個類別包含三個點。

後續將使用的函式 cv::ml::SVM::train 要求訓練資料儲存為浮點型的 cv::Mat 物件。因此，我們從上面定義的陣列中建立這些物件：

設定SVM引數

在本教程中，我們介紹了SVM在最簡單情況下的理論，即訓練樣本分為兩個線性可分的類別。然而，SVM可以用於各種各樣的問題（例如，非線性可分資料的問題，使用核函式提高樣本維度的SVM等）。因此，在訓練SVM之前，我們必須定義一些引數。這些引數儲存在 cv::ml::SVM 類的一個物件中。

在這裡

SVM 型別。我們在此選擇 C_SVC 型別，它可用於 n 類分類 (n \(\geq\) 2)。這種型別的重要特性是它能處理不完美分離的類別（即，當訓練資料非線性可分時）。此特性在這裡並不重要，因為資料是線性可分的，我們選擇此SVM型別僅因為它最常用。
SVM 核函式型別。我們沒有討論核函式，因為它們對我們正在處理的訓練資料不感興趣。然而，現在讓我們簡要解釋一下核函式背後的主要思想。它是一種對訓練資料進行的對映，旨在提高其與線性可分資料集的相似性。這種對映透過增加資料的維度來實現，並使用核函式高效地完成。我們在這裡選擇 LINEAR 型別，這意味著不進行任何對映。此引數使用 cv::ml::SVM::setKernel 定義。
演算法終止標準。SVM 訓練過程是透過迭代方式解決一個受約束的二次最佳化問題來實現的。這裡我們指定了最大迭代次數和容忍誤差，這樣即使最優超平面尚未計算出來，我們也允許演算法在更少的步驟中完成。此引數在 cv::TermCriteria 結構中定義。
訓練SVM 我們呼叫方法 cv::ml::SVM::train 來構建SVM模型。

SVM分類的區域

方法 cv::ml::SVM::predict 用於使用訓練好的SVM對輸入樣本進行分類。在此示例中，我們使用此方法根據SVM的預測結果對空間進行著色。換句話說，遍歷影像並將其畫素解釋為笛卡爾平面上的點。每個點根據SVM預測的類別進行著色；如果預測類別為1，則為綠色；如果預測類別為-1，則為藍色。

支援向量

我們這裡使用了幾個方法來獲取關於支援向量的資訊。方法 cv::ml::SVM::getSupportVectors 獲取所有支援向量。我們在這裡使用這些方法來找到作為支援向量的訓練樣本並將其突出顯示。


原始作者	Fernando Iglesias García
相容性	OpenCV >= 3.0