光流

目錄

• 目標
• 光流
  • Lucas-Kanade 方法
• OpenCV 中的 Lucas-Kanade 光流
• OpenCV 中的稠密光流

上一個教程： 均值漂移和 Camshift
下一個教程： 級聯分類器

目標

在本章中，

• 我們將理解光流的概念及其使用 Lucas-Kanade 方法進行估計。
• 我們將使用 cv.calcOpticalFlowPyrLK() 等函式來跟蹤影片中的特徵點。
• 我們將使用 cv.calcOpticalFlowFarneback() 方法建立一個稠密光流場。

光流

光流是影像物件在連續兩幀之間由於物體或攝像機運動而產生的表觀運動模式。它是一個二維向量場，其中每個向量都是一個位移向量，顯示了點從第一幀到第二幀的移動。考慮下圖（圖片來源：維基百科光流文章）。

image

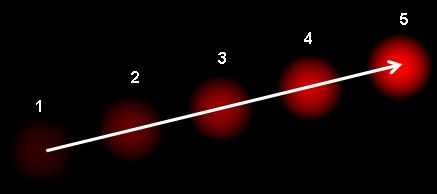
它顯示了一個球在5個連續幀中的運動。箭頭顯示了它的位移向量。光流在許多領域都有應用，例如

• 從運動中恢復結構
• 影片壓縮
• 影片穩定 ...

光流基於以下幾個假設：

1. 物件的畫素強度在連續幀之間不會改變。
2. 相鄰畫素具有相似的運動。

考慮第一幀中的畫素 \(I(x,y,t)\)（注意，這裡添加了一個新維度：時間。之前我們只處理影像，所以不需要時間）。它在 \(dt\) 時間後的下一幀中移動了距離 \((dx,dy)\)。因此，由於這些畫素是相同的且強度不變，我們可以說，

\[I(x,y,t) = I(x+dx, y+dy, t+dt)\]

然後對右側進行泰勒級數近似，去掉相同項併除以 \(dt\)，得到以下方程

\[f_x u + f_y v + f_t = 0 \;\]

其中

\[f_x = \frac{\partial f}{\partial x} \; ; \; f_y = \frac{\partial f}{\partial y}\]

\[u = \frac{dx}{dt} \; ; \; v = \frac{dy}{dt}\]

上述方程稱為光流方程。在其中，我們可以找到 \(f_x\) 和 \(f_y\)，它們是影像梯度。類似地，\(f_t\) 是沿時間的梯度。但 \((u,v)\) 是未知量。我們無法用兩個未知變數求解這個方程。因此，提供了幾種方法來解決這個問題，其中之一就是 Lucas-Kanade 方法。

Lucas-Kanade 方法

我們之前見過一個假設，即所有相鄰畫素將具有相似的運動。Lucas-Kanade 方法在點周圍取一個 3x3 的影像塊。因此，所有 9 個點都具有相同的運動。我們可以找到這 9 個點的 \((f_x, f_y, f_t)\)。所以現在我們的問題變成了求解一個包含兩個未知變數的 9 個方程組，這是一個超定系統。使用最小二乘擬合方法可以獲得更好的解決方案。下面是最終的解決方案，它是一個二方程兩未知量問題，求解即可得到答案。

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix} - \sum_{i}{f_{x_i} f_{t_i}} \\ - \sum_{i}{f_{y_i} f_{t_i}} \end{bmatrix}\]

（檢查逆矩陣與 Harris 角點檢測器的相似性。它表明角點是更好的跟蹤點。）

因此，從使用者角度來看，這個想法很簡單，我們提供一些點來跟蹤，然後接收這些點的光流向量。但仍然存在一些問題。到目前為止，我們只處理小範圍運動，因此當運動幅度較大時，它會失效。為了解決這個問題，我們使用金字塔。當我們沿著金字塔向上時，小範圍運動會被消除，大範圍運動會變成小範圍運動。因此，透過在那裡應用 Lucas-Kanade 方法，我們可以獲得光流以及尺度資訊。

OpenCV 中的 Lucas-Kanade 光流

OpenCV 將所有這些功能整合在一個函式中：cv.calcOpticalFlowPyrLK()。在這裡，我們建立一個簡單的應用程式來跟蹤影片中的某些點。為了確定這些點，我們使用 cv.goodFeaturesToTrack()。我們獲取第一幀，在其中檢測一些 Shi-Tomasi 角點，然後使用 Lucas-Kanade 光流迭代跟蹤這些點。對於函式 cv.calcOpticalFlowPyrLK()，我們傳入前一幀、前一個點和下一幀。它返回下一個點以及一些狀態數字，如果找到下一個點，則狀態值為 1，否則為 0。我們迭代地將這些下一個點作為前一個點在下一步中傳遞。請參閱下面的程式碼。

C++

• 可下載程式碼：點選此處
• 程式碼速覽

  #include <iostream>
  #include <opencv2/core.hpp>
  #include <opencv2/highgui.hpp>
  #include <opencv2/imgproc.hpp>
  #include <opencv2/videoio.hpp>
  #include <opencv2/video.hpp>
   
  using namespace cv;
  using namespace std;
   
  int main(int argc, char **argv)
  {
      const string about =
          "This sample demonstrates Lucas-Kanade Optical Flow calculation.\n"
          "The example file can be downloaded from:\n"
          " https://www.bogotobogo.com/python/OpenCV_Python/images/mean_shift_tracking/slow_traffic_small.mp4";
      const string keys =
          "{ h help | | 列印此幫助訊息 }"
          "{ @image | vtest.avi | path to image file }";
      CommandLineParser parser(argc, argv, keys);
  parser.about(about);
      if (parser.has("help"))
      {
  parser.printMessage();
          return 0;
      }
      string filename = samples::findFile(parser.get<string>("@image"));
      if (!parser.check())
      {
  parser.printErrors();
          return 0;
      }
   
      VideoCapture capture(filename);
      if (!capture.isOpened()){
          //error in opening the video input
  cerr << "Unable to open file!" << endl;
          return 0;
      }
   
      // Create some random colors
  vector<Scalar> colors;
      RNG rng;
      for(int i = 0; i < 100; i++)
      {
          int r = rng.uniform(0, 256);
          int g = rng.uniform(0, 256);
          int b = rng.uniform(0, 256);
  colors.emplace_back(r,g,b);
      }
   
      Mat old_frame, old_gray;
  vector<Point2f> p0, p1;
   
      // Take first frame and find corners in it
  capture >> old_frame;
      cvtColor(old_frame, old_gray, COLOR_BGR2GRAY);
      goodFeaturesToTrack(old_gray, p0, 100, 0.3, 7, Mat(), 7, false, 0.04);
   
      // Create a mask image for drawing purposes
      Mat mask = Mat::zeros(old_frame.size(), old_frame.type());
   
      while(true){
          Mat frame, frame_gray;
   
  capture >> frame;
          if (frame.empty())
              break;
          cvtColor(frame, frame_gray, COLOR_BGR2GRAY);
   
          // calculate optical flow
  vector<uchar> status;
  vector<float> err;
          TermCriteria criteria = TermCriteria((TermCriteria::COUNT) + (TermCriteria::EPS), 10, 0.03);
          calcOpticalFlowPyrLK(old_gray, frame_gray, p0, p1, status, err, Size(15,15), 2, criteria);
   
  vector<Point2f> good_new;
          for(uint i = 0; i < p0.size(); i++)
          {
              // Select good points
              if(status[i] == 1) {
  good_new.push_back(p1[i]);
                  // draw the tracks
                  line(mask,p1[i], p0[i], colors[i], 2);
                  circle(frame, p1[i], 5, colors[i], -1);
              }
          }
          Mat img;
          add(frame, mask, img);
   
          imshow("Frame", img);
   
          int keyboard = waitKey(30);
          if (keyboard == 'q' || keyboard == 27)
              break;
   
          // Now update the previous frame and previous points
  old_gray = frame_gray.clone();
  p0 = good_new;
      }
  }

Python

• 可下載程式碼：點選此處
• 程式碼速覽

  import numpy as np
  import cv2 as cv
  import argparse
   
  parser = argparse.ArgumentParser(description='This sample demonstrates Lucas-Kanade Optical Flow calculation. \
  The example file can be downloaded from: \
  https://www.bogotobogo.com/python/OpenCV_Python/images/mean_shift_tracking/slow_traffic_small.mp4')
  parser.add_argument('image', type=str, help='path to image file')
  args = parser.parse_args()
   
  cap = cv.VideoCapture(args.image)
   
  # params for ShiTomasi corner detection
  feature_params = dict( maxCorners = 100,
  qualityLevel = 0.3,
  minDistance = 7,
  blockSize = 7 )
   
  # Parameters for lucas kanade optical flow
  lk_params = dict( winSize = (15, 15),
  maxLevel = 2,
  criteria = (cv.TERM_CRITERIA_EPS | cv.TERM_CRITERIA_COUNT, 10, 0.03))
   
  # Create some random colors
  color = np.random.randint(0, 255, (100, 3))
   
  # Take first frame and find corners in it
  ret, old_frame = cap.read()
  old_gray = cv.cvtColor(old_frame, cv.COLOR_BGR2GRAY)
  p0 = cv.goodFeaturesToTrack(old_gray, mask = None, **feature_params)
   
  # Create a mask image for drawing purposes
  mask = np.zeros_like(old_frame)
   
  while(1)
  ret, frame = cap.read()
      if not ret
  print('No frames grabbed!')
          break
   
  frame_gray = cv.cvtColor(frame, cv.COLOR_BGR2GRAY)
   
      # calculate optical flow
  p1, st, err = cv.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
   
      # Select good points
      if p1 is not None
  good_new = p1[st==1]
  good_old = p0[st==1]
   
      # draw the tracks
      for i, (new, old) in enumerate(zip(good_new, good_old))
  a, b = new.ravel()
  c, d = old.ravel()
  mask = cv.line(mask, (int(a), int(b)), (int(c), int(d)), color[i].tolist(), 2)
  frame = cv.circle(frame, (int(a), int(b)), 5, color[i].tolist(), -1)
  img = cv.add(frame, mask)
   
      cv.imshow('frame', img)
  k = cv.waitKey(30) & 0xff
      if k == 27
          break
   
      # Now update the previous frame and previous points
  old_gray = frame_gray.copy()
  p0 = good_new.reshape(-1, 1, 2)
   
  cv.destroyAllWindows()

Java

• 可下載程式碼：點選此處
• 程式碼速覽

  import java.util.ArrayList;
  import java.util.Random;
  import org.opencv.core.*;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgproc.Imgproc;
  import org.opencv.video.Video;
  import org.opencv.videoio.VideoCapture;
   
  class OptFlow {
      public void run(String[] args) {
  String filename = args[0];
  VideoCapture capture = new VideoCapture(filename);
          if (!capture.isOpened()) {
  System.out.println("Unable to open this file");
  System.exit(-1);
          }
   
   
          // Create some random colors
  Scalar[] colors = new Scalar[100];
  Random rng = new Random();
          for (int i = 0 ; i < 100 ; i++) {
              int r = rng.nextInt(256);
              int g = rng.nextInt(256);
              int b = rng.nextInt(256);
  colors[i] = new Scalar(r, g, b);
          }
   
  Mat old_frame = new Mat() , old_gray = new Mat();
   
          // Since the function Imgproc.goodFeaturesToTrack requires MatofPoint
          // therefore first p0MatofPoint is passed to the function and then converted to MatOfPoint2f
  MatOfPoint p0MatofPoint = new MatOfPoint();
  capture.read(old_frame);
  Imgproc.cvtColor(old_frame, old_gray, Imgproc.COLOR_BGR2GRAY);
  Imgproc.goodFeaturesToTrack(old_gray, p0MatofPoint,100,0.3,7, new Mat(),7,false,0.04);
   
  MatOfPoint2f p0 = new MatOfPoint2f(p0MatofPoint.toArray()) , p1 = new MatOfPoint2f();
   
          // Create a mask image for drawing purposes
  Mat mask = Mat.zeros(old_frame.size(), old_frame.type());
   
          while (true) {
  Mat frame = new Mat(), frame_gray = new Mat();
  capture.read(frame);
              if (frame.empty()) {
                  break;
              }
   
  Imgproc.cvtColor(frame, frame_gray, Imgproc.COLOR_BGR2GRAY);
   
              // calculate optical flow
  MatOfByte status = new MatOfByte();
  MatOfFloat err = new MatOfFloat();
  TermCriteria criteria = new TermCriteria(TermCriteria.COUNT + TermCriteria.EPS,10,0.03);
  Video.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, p1, status, err, new Size(15,15),2, criteria);
   
              byte StatusArr[] = status.toArray();
  Point p0Arr[] = p0.toArray();
  Point p1Arr[] = p1.toArray();
  ArrayList<Point> good_new = new ArrayList<>();
   
              for (int i = 0; i<StatusArr.length ; i++ ) {
                  if (StatusArr[i] == 1) {
  good_new.add(p1Arr[i]);
  Imgproc.line(mask, p1Arr[i], p0Arr[i], colors[i],2);
  Imgproc.circle(frame, p1Arr[i],5, colors[i],-1);
                  }
              }
   
  Mat img = new Mat();
  Core.add(frame, mask, img);
   
  HighGui.imshow("Frame", img);
   
              int keyboard = HighGui.waitKey(30);
              if (keyboard == 'q' || keyboard == 27) {
                  break;
              }
   
              // Now update the previous frame and previous points
  old_gray = frame_gray.clone();
              Point[] good_new_arr = new Point[good_new.size()];
  good_new_arr = good_new.toArray(good_new_arr);
  p0 = new MatOfPoint2f(good_new_arr);
          }
  System.exit(0);
      }
  }
   
  public class OpticalFlowDemo {
      public static void main(String[] args) {
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
          new OptFlow().run(args);
      }
  }

（此程式碼不檢查下一個關鍵點的正確性。因此，即使影像中的任何特徵點消失，光流也有可能找到看起來與其接近的下一個點。所以，實際上為了進行穩健的跟蹤，應該以特定的間隔檢測角點。OpenCV 示例中包含這樣一個示例，它每 5 幀查詢一次特徵點。它還會對獲得的光流點進行反向檢查，以僅選擇好的點。請檢視 samples/python/lk_track.py）。

檢視我們得到的結果

image

OpenCV 中的稠密光流

Lucas-Kanade 方法計算稀疏特徵集（在我們的示例中，是使用 Shi-Tomasi 演算法檢測到的角點）的光流。OpenCV 提供了另一種演算法來查詢稠密光流。它計算幀中所有點的光流。該演算法基於 Gunnar Farneback 在 2003 年的論文《基於多項式展開的雙幀運動估計》中解釋的 Gunnar Farneback 演算法。

以下示例展示瞭如何使用上述演算法查詢稠密光流。我們獲得一個包含光流向量 \((u,v)\) 的雙通道陣列。我們計算它們的幅度和方向。為了更好的視覺化，我們對結果進行了顏色編碼。方向對應於影像的色相值。幅度對應於亮度平面。請參閱下面的程式碼。

C++

• 可下載程式碼：點選此處
• 程式碼速覽

  #include <iostream>
  #include <opencv2/core.hpp>
  #include <opencv2/highgui.hpp>
  #include <opencv2/imgproc.hpp>
  #include <opencv2/videoio.hpp>
  #include <opencv2/video.hpp>
   
  using namespace cv;
  using namespace std;
   
  int main()
  {
      VideoCapture capture(samples::findFile("vtest.avi"));
      if (!capture.isOpened()){
          //error in opening the video input
  cerr << "Unable to open file!" << endl;
          return 0;
      }
   
      Mat frame1, prvs;
  capture >> frame1;
  cvtColor(frame1, prvs, COLOR_BGR2GRAY);
   
      while(true){
          Mat frame2, next;
  capture >> frame2;
          if (frame2.empty())
              break;
  cvtColor(frame2, next, COLOR_BGR2GRAY);
   
          Mat flow(prvs.size(), CV_32FC2);
  calcOpticalFlowFarneback(prvs, next, flow, 0.5, 3, 15, 3, 5, 1.2, 0);
   
          // visualization
          Mat flow_parts[2];
  split(flow, flow_parts);
          Mat magnitude, angle, magn_norm;
  cartToPolar(flow_parts[0], flow_parts[1], magnitude, angle, true);
  normalize(magnitude, magn_norm, 0.0f, 1.0f, NORM_MINMAX);
  angle *= ((1.f / 360.f) * (180.f / 255.f));
   
          //build hsv image
          Mat _hsv[3], hsv, hsv8, bgr;
  _hsv[0] = angle;
  _hsv[1] = Mat::ones(angle.size(), CV_32F);
  _hsv[2] = magn_norm;
  merge(_hsv, 3, hsv);
  hsv.convertTo(hsv8, CV_8U, 255.0);
  cvtColor(hsv8, bgr, COLOR_HSV2BGR);
   
  imshow("frame2", bgr);
   
          int keyboard = waitKey(30);
          if (keyboard == 'q' || keyboard == 27)
              break;
   
  prvs = next;
      }
  }

Python

• 可下載程式碼：點選此處
• 程式碼速覽

  import numpy as np
  import cv2 as cv
  cap = cv.VideoCapture(cv.samples.findFile("vtest.avi"))
  ret, frame1 = cap.read()
  prvs = cv.cvtColor(frame1, cv.COLOR_BGR2GRAY)
  hsv = np.zeros_like(frame1)
  hsv[..., 1] = 255
  while(1)
  ret, frame2 = cap.read()
      if not ret
  print('No frames grabbed!')
          break
   
  next = cv.cvtColor(frame2, cv.COLOR_BGR2GRAY)
  flow = cv.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
  mag, ang = cv.cartToPolar(flow[..., 0], flow[..., 1])
  hsv[..., 0] = ang*180/np.pi/2
  hsv[..., 2] = cv.normalize(mag, None, 0, 255, cv.NORM_MINMAX)
  bgr = cv.cvtColor(hsv, cv.COLOR_HSV2BGR)
      cv.imshow('frame2', bgr)
  k = cv.waitKey(30) & 0xff
      if k == 27
          break
      elif k == ord('s')
          cv.imwrite('opticalfb.png', frame2)
          cv.imwrite('opticalhsv.png', bgr)
  prvs = next
   
  cv.destroyAllWindows()

Java

• 可下載程式碼：點選此處
• 程式碼速覽

  import java.util.ArrayList;
  import org.opencv.core.*;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgproc.Imgproc;
  import org.opencv.video.Video;
  import org.opencv.videoio.VideoCapture;
   
   
  class OptFlowDense {
      public void run(String[] args) {
  String filename = args[0];
  VideoCapture capture = new VideoCapture(filename);
          if (!capture.isOpened()) {
              //error in opening the video input
  System.out.println("Unable to open file!");
  System.exit(-1);
          }
   
  Mat frame1 = new Mat() , prvs = new Mat();
  capture.read(frame1);
  Imgproc.cvtColor(frame1, prvs, Imgproc.COLOR_BGR2GRAY);
   
          while (true) {
  Mat frame2 = new Mat(), next = new Mat();
  capture.read(frame2);
              if (frame2.empty()) {
                  break;
              }
  Imgproc.cvtColor(frame2, next, Imgproc.COLOR_BGR2GRAY);
   
  Mat flow = new Mat(prvs.size(), CvType.CV_32FC2);
  Video.calcOpticalFlowFarneback(prvs, next, flow,0.5,3,15,3,5,1.2,0);
   
              // visualization
  ArrayList<Mat> flow_parts = new ArrayList<>(2);
  Core.split(flow, flow_parts);
  Mat magnitude = new Mat(), angle = new Mat(), magn_norm = new Mat();
  Core.cartToPolar(flow_parts.get(0), flow_parts.get(1), magnitude, angle,true);
  Core.normalize(magnitude, magn_norm,0.0,1.0, Core.NORM_MINMAX);
              float factor = (float) ((1.0/360.0)*(180.0/255.0));
  Mat new_angle = new Mat();
  Core.multiply(angle, new Scalar(factor), new_angle);
   
              //build hsv image
  ArrayList<Mat> _hsv = new ArrayList<>() ;
  Mat hsv = new Mat(), hsv8 = new Mat(), bgr = new Mat();
   
  _hsv.add(new_angle);
  _hsv.add(Mat.ones(angle.size(), CvType.CV_32F));
  _hsv.add(magn_norm);
  Core.merge(_hsv, hsv);
  hsv.convertTo(hsv8, CvType.CV_8U, 255.0);
  Imgproc.cvtColor(hsv8, bgr, Imgproc.COLOR_HSV2BGR);
   
  HighGui.imshow("frame2", bgr);
   
              int keyboard = HighGui.waitKey(30);
              if (keyboard == 'q' || keyboard == 27) {
                  break;
              }
  prvs = next;
          }
  System.exit(0);
      }
  }
   
  public class OpticalFlowDenseDemo {
      public static void main(String[] args) {
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
          new OptFlowDense().run(args);
      }
  }

請參閱下面的結果

image