Harris 角點檢測器

目錄

• 目標
• 理論
  • 什麼是特徵？
  • 影像特徵的型別
  • 為什麼角點如此特殊？
  • 它是如何工作的？
• 程式碼
• 解釋
• 結果

下一教程： Shi-Tomasi 角點檢測器

原始作者	Ana Huamán
相容性	OpenCV >= 3.0

目標

在本教程中，您將學習

• 什麼是特徵以及它們為何重要
• 使用函式 cv::cornerHarris 使用 Harris-Stephens 方法檢測角點。

理論

什麼是特徵？

• 在計算機視覺中，通常我們需要找到環境中不同幀之間的匹配點。為什麼？如果我們知道兩幅影像如何相互關聯，我們就可以使用*這兩幅*影像來提取它們的資訊。
• 當我們說 匹配點 時，通常是指場景中我們容易識別的 特性。我們稱這些特性為 特徵。
• 那麼，特徵應該具備哪些特性呢？
  • 它必須是 *唯一可識別的*

影像特徵的型別

列舉如下

• 邊緣
• 角點 (也稱為興趣點)
• 斑點 (也稱為興趣區域)

在本教程中，我們將專門研究 角點 特徵。

為什麼角點如此特殊？

• 因為角點是兩條邊緣的交點，它代表一個方向 改變 的點。因此，影像的梯度（在兩個方向上）具有很大的變化，這可以用於檢測它。

它是如何工作的？

• 讓我們尋找角點。由於角點代表影像中梯度的變化，我們將尋找這種“變化”。

• 考慮一幅灰度影像 \(I\)。我們將用一個視窗 \(w(x,y)\) （在 x 方向有 \(u\) 位移，在 y 方向有 \(v\) 位移）掃過 \(I\)，並計算強度變化。

  \[E(u,v) = \sum _{x,y} w(x,y)[ I(x+u,y+v) - I(x,y)]^{2}\]

  其中

  • \(w(x,y)\) 是在位置 \((x,y)\) 的視窗
  • \(I(x,y)\) 是在 \((x,y)\) 的強度
  • \(I(x+u,y+v)\) 是在移動後的視窗 \((x+u,y+v)\) 的強度

• 由於我們尋找帶有角點的視窗，因此我們尋找強度變化大的視窗。因此，我們必須使上述方程最大化，特別是以下項：

  \[\sum _{x,y}[ I(x+u,y+v) - I(x,y)]^{2}\]

• 使用 泰勒展開

  \[E(u,v) \approx \sum _{x,y}[ I(x,y) + u I_{x} + vI_{y} - I(x,y)]^{2}\]

• 展開方程並適當消去項

  \[E(u,v) \approx \sum _{x,y} u^{2}I_{x}^{2} + 2uvI_{x}I_{y} + v^{2}I_{y}^{2}\]

• 可以矩陣形式表示為

  \[E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} \left ( \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \right ) \begin{bmatrix} u \\ v \end{bmatrix}\]

• 我們記為

  \[M = \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix}\]

• 因此，我們的方程現在是

  \[E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix}\]

• 為每個視窗計算一個分數，以確定它是否可能包含一個角點

  \[R = det(M) - k(trace(M))^{2}\]

  其中

  • det(M) = \(\lambda_{1}\lambda_{2}\)
  • trace(M) = \(\lambda_{1}+\lambda_{2}\)

  一個得分 \(R\) 大於某個特定值的視窗被視為“角點”

程式碼

C++

本教程的程式碼顯示在以下行中。您也可以從此處下載。

 
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <iostream>
 
using namespace cv;
using namespace std;
 
Mat src, src_gray;
int thresh = 200;
int max_thresh = 255;
 
const char* source_window = "Source image";
const char* corners_window = "Corners detected";
 
void cornerHarris_demo( int, void* );
 
int main( int argc, char** argv )
{
    CommandLineParser parser( argc, argv, "{@input | building.jpg | input image}" );
src = imread( samples::findFile( parser.get<String>( "@input" ) ) );
    if ( src.empty() )
    {
cout << "Could not open or find the image!\n" << endl;
cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
    }
cvtColor( src, src_gray, COLOR_BGR2GRAY );
 
namedWindow( source_window );
createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo );
imshow( source_window, src );
 
cornerHarris_demo( 0, 0 );
 
cv::Mat::empty
    return 0;
}
 
void cornerHarris_demo( int, void* )
{
    int blockSize = 2;
    int apertureSize = 3;
    double k = 0.04;
 
    Mat dst = Mat::zeros( src.size(), CV_32FC1 );
cornerHarris( src_gray, dst, blockSize, apertureSize, k );
 
    Mat dst_norm, dst_norm_scaled;
normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
convertScaleAbs( dst_norm, dst_norm_scaled );
 
    for( int i = 0; i < dst_norm.rows ; i++ )
    {
        for( int j = 0; j < dst_norm.cols; j++ )
        {
            if( (int) dst_norm.at<float>(i,j) > thresh )
            {
circle( dst_norm_scaled, Point(j,i), 5, Scalar(0), 2, 8, 0 );
            }
        }
    }
 
    namedWindow( corners_window );
    imshow( corners_window, dst_norm_scaled );
}

Java

本教程的程式碼顯示在以下行中。您也可以從此處下載。

import java.awt.BorderLayout;
import java.awt.Container;
import java.awt.Image;
 
import javax.swing.BoxLayout;
import javax.swing.ImageIcon;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JPanel;
import javax.swing.JSlider;
import javax.swing.event.ChangeEvent;
import javax.swing.event.ChangeListener;
 
import org.opencv.core.Core;
import org.opencv.core.CvType;
import org.opencv.core.Mat;
import org.opencv.core.Point;
import org.opencv.core.Scalar;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
 
class CornerHarris {
    private Mat srcGray = new Mat();
    private Mat dst = new Mat();
    private Mat dstNorm = new Mat();
    private Mat dstNormScaled = new Mat();
    private JFrame frame;
    private JLabel imgLabel;
    private JLabel cornerLabel;
    private static final int MAX_THRESHOLD = 255;
    private int threshold = 200;
 
    public CornerHarris(String[] args) {
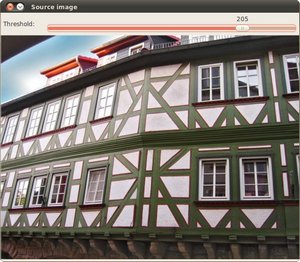
String filename = args.length > 0 ? args[0] : "../data/building.jpg";
Mat src = Imgcodecs.imread(filename);
        if (src.empty()) {
System.err.println("Cannot read image: " + filename);
System.exit(0);
        }
 
Imgproc.cvtColor(src, srcGray, Imgproc.COLOR_BGR2GRAY);
 
        // Create and set up the window.
frame = new JFrame("Harris corner detector demo");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
        // Set up the content pane.
Image img = HighGui.toBufferedImage(src);
addComponentsToPane(frame.getContentPane(), img);
        // Use the content pane's default BorderLayout. No need for
        // setLayout(new BorderLayout());
        // Display the window.
frame.pack();
frame.setVisible(true);
update();
    }
 
    private void addComponentsToPane(Container pane, Image img) {
        if (!(pane.getLayout() instanceof BorderLayout)) {
pane.add(new JLabel("Container doesn't use BorderLayout!"));
            return;
        }
 
JPanel sliderPanel = new JPanel();
sliderPanel.setLayout(new BoxLayout(sliderPanel, BoxLayout.PAGE_AXIS));
 
sliderPanel.add(new JLabel("Threshold: "));
JSlider slider = new JSlider(0, MAX_THRESHOLD, threshold);
slider.setMajorTickSpacing(20);
slider.setMinorTickSpacing(10);
slider.setPaintTicks(true);
slider.setPaintLabels(true);
slider.addChangeListener(new ChangeListener() {
@Override
            public void stateChanged(ChangeEvent e) {
JSlider source = (JSlider) e.getSource();
threshold = source.getValue();
update();
            }
        });
sliderPanel.add(slider);
pane.add(sliderPanel, BorderLayout.PAGE_START);
 
JPanel imgPanel = new JPanel();
imgLabel = new JLabel(new ImageIcon(img));
imgPanel.add(imgLabel);
 
Mat blackImg = Mat.zeros(srcGray.size(), CvType.CV_8U);
cornerLabel = new JLabel(new ImageIcon(HighGui.toBufferedImage(blackImg)));
imgPanel.add(cornerLabel);
 
pane.add(imgPanel, BorderLayout.CENTER);
    }
 
    private void update() {
dst = Mat.zeros(srcGray.size(), CvType.CV_32F);
 
        int blockSize = 2;
        int apertureSize = 3;
        double k = 0.04;
 
Imgproc.cornerHarris(srcGray, dst, blockSize, apertureSize, k);
 
Core.normalize(dst, dstNorm, 0, 255, Core.NORM_MINMAX);
Core.convertScaleAbs(dstNorm, dstNormScaled);
 
        float[] dstNormData = new float[(int) (dstNorm.total() * dstNorm.channels())];
dstNorm.get(0, 0, dstNormData);
 
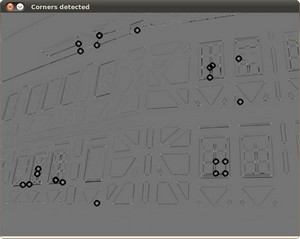
        for (int i = 0; i < dstNorm.rows(); i++) {
            for (int j = 0; j < dstNorm.cols(); j++) {
                if ((int) dstNormData[i * dstNorm.cols() + j] > threshold) {
Imgproc.circle(dstNormScaled, new Point(j, i), 5, new Scalar(0), 2, 8, 0);
                }
            }
        }
 
cornerLabel.setIcon(new ImageIcon(HighGui.toBufferedImage(dstNormScaled)));
frame.repaint();
    }
}
 
public class CornerHarrisDemo {
    public static void main(String[] args) {
        // 載入本地 OpenCV 庫
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
 
        // Schedule a job for the event dispatch thread
        // creating and showing this application's GUI.
javax.swing.SwingUtilities.invokeLater(new Runnable() {
@Override
            public void run() {
                new CornerHarris(args);
            }
        });
    }
}

Python

本教程的程式碼顯示在以下行中。您也可以從此處下載。

from __future__ import print_function
import cv2 as cv
import numpy as np
import argparse
 
source_window = 'Source image'
corners_window = 'Corners detected'
max_thresh = 255
 
def cornerHarris_demo(val)
thresh = val
 
    # Detector parameters
blockSize = 2
apertureSize = 3
k = 0.04
 
    # Detecting corners
dst = cv.cornerHarris(src_gray, blockSize, apertureSize, k)
 
    # Normalizing
dst_norm = np.empty(dst.shape, dtype=np.float32)
    cv.normalize(dst, dst_norm, alpha=0, beta=255, norm_type=cv.NORM_MINMAX)
dst_norm_scaled = cv.convertScaleAbs(dst_norm)
 
    # Drawing a circle around corners
    for i in range(dst_norm.shape[0])
        for j in range(dst_norm.shape[1])
            if int(dst_norm[i,j]) > thresh
                cv.circle(dst_norm_scaled, (j,i), 5, (0), 2)
 
    # Showing the result
    cv.namedWindow(corners_window)
    cv.imshow(corners_window, dst_norm_scaled)
 
# 載入源影像並將其轉換為灰度影像
parser = argparse.ArgumentParser(description='Code for Harris corner detector tutorial.')
parser.add_argument('--input', help='Path to input image.', default='building.jpg')
args = parser.parse_args()
 
src = cv.imread(cv.samples.findFile(args.input))
if src is None
print('Could not open or find the image:', args.input)
exit(0)
 
src_gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
 
# 建立視窗和軌跡欄
cv.namedWindow(source_window)
thresh = 200 # initial threshold
cv.createTrackbar('Threshold: ', source_window, thresh, max_thresh, cornerHarris_demo)
cv.imshow(source_window, src)
cornerHarris_demo(thresh)
 
cv.waitKey()

解釋

結果

原始影像

檢測到的角點被小黑圈包圍