Sobel 導數

目錄

• 目標
• 理論
  • Sobel 運算元
  • 公式
• 程式碼
• 解釋
  • 宣告變數
  • 載入源影像
  • 降噪
  • 灰度化
  • Sobel 運算元
  • 將輸出轉換為 CV_8U 影像
  • 梯度
  • 顯示結果
• 結果

上一教程： 為影像新增邊框
下一教程： 拉普拉斯運算元

原始作者	Ana Huamán
相容性	OpenCV >= 3.0

目標

在本教程中，您將學習如何

• 使用 OpenCV 函式 Sobel() 計算影像的導數。
• 使用 OpenCV 函式 Scharr() 計算尺寸為 \(3 \cdot 3\) 的核的更精確導數

理論

注意

以下解釋摘自 Bradski 和 Kaehler 所著的 Learning OpenCV 一書。

1. 在前面兩個教程中，我們看到了卷積的應用示例。最重要的卷積之一是計算影像中的導數（或其近似值）。
2. 為什麼影像中導數的計算可能很重要？假設我們想檢測影像中存在的邊緣。例如

您可以很容易地注意到，在邊緣處，畫素強度會顯著變化。表達變化的好方法是使用導數。梯度的高變化表示影像中的重大變化。

1. 為了更形象化，假設我們有一個一維影像。邊緣由下方圖中強度的“跳躍”顯示

1. 如果我們取一階導數（實際上，這裡顯示為一個最大值），邊緣的“跳躍”會更容易看到

1. 因此，從上面的解釋我們可以推斷，檢測影像邊緣的方法可以透過定位梯度高於其鄰居（或者更普遍地說，高於閾值）的畫素位置來實現。
2. 更詳細的解釋，請參考 Bradski 和 Kaehler 所著的 Learning OpenCV

Sobel 運算元

1. Sobel 運算元是一種離散微分運算元。它計算影像強度函式的梯度的近似值。
2. Sobel 運算元結合了高斯平滑和微分。

公式

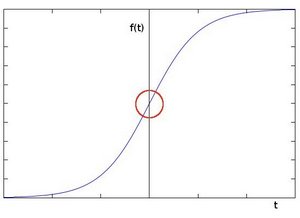
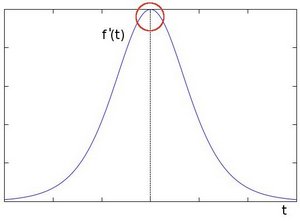
假設待操作影像為 \(I\)

1. 我們計算兩個導數

   1. 水平變化：這是透過將 \(I\) 與一個奇數尺寸的核 \(G_{x}\) 進行卷積來計算的。例如，對於尺寸為 3 的核，\(G_{x}\) 將按如下方式計算：

   \[G_{x} = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} * I\]

   1. 垂直變化：這是透過將 \(I\) 與一個奇數尺寸的核 \(G_{y}\) 進行卷積來計算的。例如，對於尺寸為 3 的核，\(G_{y}\) 將按如下方式計算：

   \[G_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} * I\]

2. 在影像的每個點，我們透過結合上述兩個結果來計算該點梯度的近似值

   \[G = \sqrt{ G_{x}^{2} + G_{y}^{2} }\]

   儘管有時會使用以下更簡單的方程

   \[G = |G_{x}| + |G_{y}|\]

注意

當核大小為 3 時，上面顯示的 Sobel 核可能會產生明顯的誤差（畢竟，Sobel 只是導數的近似）。OpenCV 透過使用 Scharr() 函式解決了尺寸為 3 的核的這種不準確性。它與標準 Sobel 函式一樣快，但更精確。它實現了以下核：

\[G_{x} = \begin{bmatrix} -3 & 0 & +3 \\ -10 & 0 & +10 \\ -3 & 0 & +3 \end{bmatrix}\]

\[G_{y} = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ +3 & +10 & +3 \end{bmatrix}\]

您可以在 OpenCV 參考手冊 - Scharr() 中檢視此函式的更多資訊。此外，在下面的示例程式碼中，您會注意到 Sobel() 函式的程式碼上方也有 Scharr() 函式的註釋程式碼。取消註釋（並顯然註釋掉 Sobel 相關程式碼）應該能讓您瞭解此函式的工作原理。

程式碼

1. 此程式的作用是什麼？
   • 應用Sobel 運算元，並生成一張以較暗背景顯示檢測到的邊緣的影像。
2. 教程程式碼如下所示。

C++

您也可以從這裡下載。

 
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
 
#include <iostream>
 
using namespace cv;
using namespace std;
 
int main( int argc, char** argv )
{
  cv::CommandLineParser parser(argc, argv,
                               "{@input |lena.jpg|輸入影像}"
                               "{ksize k|1|ksize (執行時按 'K' 鍵增加其值)}"
                               "{scale s|1|比例 (執行時按 'S' 鍵增加其值)}"
                               "{delta d|0|delta (執行時按 'D' 鍵增加其值)}"
                               "{help h|false|顯示幫助資訊}");
 
cout << "The sample uses Sobel or Scharr OpenCV functions for edge detection\n\n";
parser.printMessage();
cout << "\nPress 'ESC' to exit program.\nPress 'R' to reset values ( ksize will be -1 equal to Scharr function )";
 
  // 首先宣告我們要使用的變數
  Mat image,src, src_gray;
  Mat grad;
  const String window_name = "Sobel Demo - Simple Edge Detector";
  int ksize = parser.get<int>("ksize");
  int scale = parser.get<int>("scale");
  int delta = parser.get<int>("delta");
  int ddepth = CV_16S;
 
  String imageName = parser.get<String>("@input");
  // 像往常一樣，我們載入源影像 (src)
image = imread( samples::findFile( imageName ), IMREAD_COLOR ); // Load an image
 
  // 檢查影像是否載入成功
  if( image.empty() )
  {
printf("Error opening image: %s\n", imageName.c_str());
    return EXIT_FAILURE;
  }
 
  for (;;)
  {
    // Remove noise by blurring with a Gaussian filter ( kernel size = 3 )
GaussianBlur(image, src, Size(3, 3), 0, 0, BORDER_DEFAULT);
 
    // 將影像轉換為灰度
cvtColor(src, src_gray, COLOR_BGR2GRAY);
 
    Mat grad_x, grad_y;
    Mat abs_grad_x, abs_grad_y;
 
Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT);
 
Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT);
 
    // 轉換回 CV_8U
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);
 
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);
 
imshow(window_name, grad);
    char key = (char)waitKey(0);
 
    if(key == 27)
    {
      return EXIT_SUCCESS;
    }
 
    if (key == 'k' || key == 'K')
    {
ksize = ksize < 30 ? ksize+2 : -1;
    }
 
    if (key == 's' || key == 'S')
    {
scale++;
    }
 
    if (key == 'd' || key == 'D')
    {
delta++;
    }
 
    if (key == 'r' || key == 'R')
    {
      scale =  1;
ksize = -1;
delta = 0;
    }
  }
  return EXIT_SUCCESS;
}

Java

您也可以從這裡下載。

 
import org.opencv.core.*;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
 
class SobelDemoRun {
 
    public void run(String[] args) {
 
        // 首先宣告我們要使用的變數
Mat src, src_gray = new Mat();
Mat grad = new Mat();
String window_name = "Sobel Demo - Simple Edge Detector";
        int scale = 1;
        int delta = 0;
        int ddepth = CvType.CV_16S;
 
        // 像往常一樣，我們載入源影像 (src)
        // Check number of arguments
        if (args.length == 0){
System.out.println("Not enough parameters!");
System.out.println("Program Arguments: [image_path]");
System.exit(-1);
        }
 
        // Load the image
src = Imgcodecs.imread(args[0]);
 
        // 檢查影像是否載入成功
        if( src.empty() ) {
System.out.println("Error opening image: " + args[0]);
System.exit(-1);
        }
 
        // Remove noise by blurring with a Gaussian filter ( kernel size = 3 )
Imgproc.GaussianBlur( src, src, new Size(3, 3), 0, 0, Core.BORDER_DEFAULT );
 
        // 將影像轉換為灰度
Imgproc.cvtColor( src, src_gray, Imgproc.COLOR_RGB2GRAY );
 
Mat grad_x = new Mat(), grad_y = new Mat();
Mat abs_grad_x = new Mat(), abs_grad_y = new Mat();
 
        //Imgproc.Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, Core.BORDER_DEFAULT );
Imgproc.Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, Core.BORDER_DEFAULT );
 
        //Imgproc.Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, Core.BORDER_DEFAULT );
Imgproc.Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, Core.BORDER_DEFAULT );
 
        // 轉換回 CV_8U
Core.convertScaleAbs( grad_x, abs_grad_x );
Core.convertScaleAbs( grad_y, abs_grad_y );
 
Core.addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
 
HighGui.imshow( window_name, grad );
HighGui.waitKey(0);
 
System.exit(0);
    }
}
 
public class SobelDemo {
    public static void main(String[] args) {
        // 載入本地庫。
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
        new SobelDemoRun().run(args);
    }
}

Python

您也可以從這裡下載。

"""
@file sobel_demo.py
@brief 使用 Sobel 和/或 Scharr OpenCV 函式製作簡單邊緣檢測器的示例程式碼
"""
import sys
import cv2 as cv
 
 
def main(argv)
    
window_name = ('Sobel Demo - Simple Edge Detector')
scale = 1
delta = 0
ddepth = cv.CV_16S
    
 
    
    if len(argv) < 1
        print ('Not enough parameters')
        print ('Usage:\nmorph_lines_detection.py < path_to_image >')
        return -1
 
    # Load the image
src = cv.imread(argv[0], cv.IMREAD_COLOR)
 
    # Check if image is loaded fine
    if src is None
        print ('Error opening image: ' + argv[0])
        return -1
    
 
    
src = cv.GaussianBlur(src, (3, 3), 0)
    
 
    
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
    
 
    
grad_x = cv.Sobel(gray, ddepth, 1, 0, ksize=3, scale=scale, delta=delta, borderType=cv.BORDER_DEFAULT)
 
    # Gradient-Y
    # grad_y = cv.Scharr(gray,ddepth,0,1)
grad_y = cv.Sobel(gray, ddepth, 0, 1, ksize=3, scale=scale, delta=delta, borderType=cv.BORDER_DEFAULT)
    
 
    
abs_grad_x = cv.convertScaleAbs(grad_x)
abs_grad_y = cv.convertScaleAbs(grad_y)
    
 
    
grad = cv.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0)
    
 
    
    cv.imshow(window_name, grad)
    cv.waitKey(0)
    
 
    return 0
 
if __name__ == "__main__"
    main(sys.argv[1:])

解釋

宣告變數

  // 首先宣告我們要使用的變數
  Mat image,src, src_gray;
  Mat grad;
  const String window_name = "Sobel Demo - Simple Edge Detector";
  int ksize = parser.get<int>("ksize");
  int scale = parser.get<int>("scale");
  int delta = parser.get<int>("delta");
  int ddepth = CV_16S;

載入源影像

  String imageName = parser.get<String>("@input");
  // 像往常一樣，我們載入源影像 (src)
image = imread( samples::findFile( imageName ), IMREAD_COLOR ); // Load an image
 
  // 檢查影像是否載入成功
  if( image.empty() )
  {
printf("Error opening image: %s\n", imageName.c_str());
    return EXIT_FAILURE;
  }

降噪

    // Remove noise by blurring with a Gaussian filter ( kernel size = 3 )
    GaussianBlur(image, src, Size(3, 3), 0, 0, BORDER_DEFAULT);

灰度化

    // 將影像轉換為灰度
    cvtColor(src, src_gray, COLOR_BGR2GRAY);

Sobel 運算元

    Mat grad_x, grad_y;
    Mat abs_grad_x, abs_grad_y;
 
    Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT);
 
    Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT);

• 我們計算 x 和 y 方向的“導數”。為此，我們使用 Sobel() 函式，如下所示：該函式接受以下引數：

  • src_gray：在我們的示例中，它是輸入影像。這裡是 CV_8U
  • grad_x / grad_y ：輸出影像。
  • ddepth：輸出影像的深度。我們將其設定為 CV_16S 以避免溢位。
  • x_order：x 方向導數的階數。
  • y_order：y 方向導數的階數。
  • scale、delta 和 BORDER_DEFAULT：我們使用預設值。

  請注意，為了計算 x 方向的梯度，我們使用：\(x_{order}= 1\) 和 \(y_{order} = 0\)。對於 y 方向，我們也類似處理。

將輸出轉換為 CV_8U 影像

    // 轉換回 CV_8U
    convertScaleAbs(grad_x, abs_grad_x);
    convertScaleAbs(grad_y, abs_grad_y);

梯度

    addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);

我們嘗試透過新增兩個方向梯度來近似梯度（請注意，這根本不是精確計算！但對我們的目的來說已經足夠了）。

顯示結果

    imshow(window_name, grad);
    char key = (char)waitKey(0);

結果

1. 這是將我們的基本檢測器應用於 lena.jpg 的輸出結果：