主成分分析 (PCA) 簡介

目錄

• 目標
• 什麼是 PCA？
• 特徵向量和特徵值是如何計算的？
• 原始碼
• 解釋
• 結果

上一篇教程： 非線性可分資料的支援向量機

原始作者	Theodore Tsesmelis
相容性	OpenCV >= 3.0

目標

在本教程中，您將學習如何

• 使用 OpenCV 類 cv::PCA 來計算物件的方向。

什麼是 PCA？

主成分分析 (PCA) 是一種統計方法，用於提取資料集中最重要的特徵。

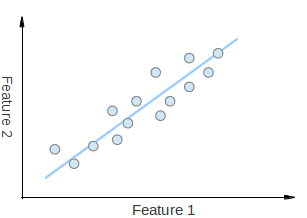
考慮圖中的一組二維點。每個維度對應一個您感興趣的特徵。有人可能會爭辯說這些點是隨機排列的。然而，如果您仔細觀察，會發現存在一個難以忽視的線性模式（由藍線指示）。PCA 的一個關鍵點是降維。降維是減少給定資料集維度數量的過程。例如，在上述情況下，可以將點集近似為一條直線，從而將給定點的維度從二維降到一維。

此外，您還可以看到這些點沿藍線的變化最大，比沿特徵 1 軸或特徵 2 軸的變化更大。這意味著如果您知道點沿藍線的位置，您將比只知道點在特徵 1 軸或特徵 2 軸上的位置擁有更多的資訊。

因此，PCA 允許我們找到資料變化最大的方向。實際上，對圖中點集執行 PCA 的結果是兩個向量，稱為特徵向量，它們是資料集的主成分。

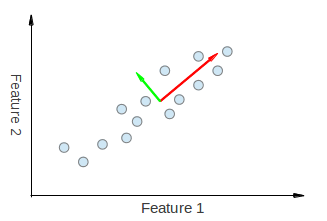
每個特徵向量的大小編碼在相應的特徵值中，並指示資料沿主成分變化的程度。特徵向量的起點是資料集中所有點的中心。將 PCA 應用於 N 維資料集會得到 N 個 N 維特徵向量、N 個特徵值和 1 個 N 維中心點。理論夠了，讓我們看看如何將這些思想付諸程式碼。

特徵向量和特徵值是如何計算的？

目標是將給定維度為 p 的資料集 X 轉換為維度更小 L 的替代資料集 Y。等效地，我們正在尋找矩陣 Y，其中 Y 是矩陣 X 的 Karhunen–Loève 變換 (KLT)

\[ \mathbf{Y} = \mathbb{K} \mathbb{L} \mathbb{T} \{\mathbf{X}\} \]

組織資料集

假設您有一個包含 p 個變數觀測值的資料集，並且您希望減少資料，使得每個觀測值僅用 L 個變數描述，其中 L < p。進一步假設資料排列為一組 n 個數據向量 \( x_1...x_n \)，其中每個 \( x_i \) 代表 p 個變數的單個分組觀測值。

• 將 \( x_1...x_n \) 寫為行向量，每個行向量有 p 列。
• 將這些行向量放入一個維度為 \( n\times p \) 的單個矩陣 X 中。

計算經驗均值

• 沿著每個維度 \( j = 1, ..., p \) 找到經驗均值。

• 將計算出的均值放入一個維度為 \( p\times 1 \) 的經驗均值向量 u 中。

  \[ \mathbf{u[j]} = \frac{1}{n}\sum_{i=1}^{n}\mathbf{X[i,j]} \]

計算與均值的偏差

均值減法是尋找使資料近似的均方誤差最小化的主成分基的解決方案中不可或缺的一部分。因此，我們透過以下方式對資料進行中心化處理：

• 從資料矩陣 X 的每一行中減去經驗均值向量 u。

• 將減去均值後的資料儲存在 \( n\times p \) 矩陣 B 中。

  \[ \mathbf{B} = \mathbf{X} - \mathbf{h}\mathbf{u^{T}} \]

  其中 h 是一個所有元素為 1 的 \( n\times 1 \) 列向量

  \[ h[i] = 1, i = 1, ..., n \]

找到協方差矩陣

• 透過矩陣 B 與自身的外積找到 \( p\times p \) 經驗協方差矩陣 C

  \[ \mathbf{C} = \frac{1}{n-1} \mathbf{B^{*}} \cdot \mathbf{B} \]

  其中 * 是共軛轉置運算子。請注意，如果 B 完全由實陣列成（許多應用中都是如此），則“共軛轉置”與常規轉置相同。

找到協方差矩陣的特徵向量和特徵值

• 計算使協方差矩陣 C 對角化的特徵向量矩陣 V

  \[ \mathbf{V^{-1}} \mathbf{C} \mathbf{V} = \mathbf{D} \]

  其中 D 是 C 的特徵值的對角矩陣。

• 矩陣 D 將採用 \( p \times p \) 對角矩陣的形式

  \[ D[k,l] = \left\{\begin{matrix} \lambda_k, k = l \\ 0, k \neq l \end{matrix}\right. \]

  這裡，\( \lambda_j \) 是協方差矩陣 C 的第 j 個特徵值

• 矩陣 V 的維度也是 p x p，包含 p 個列向量，每個向量的長度為 p，它們代表協方差矩陣 C 的 p 個特徵向量。
• 特徵值和特徵向量是成對且有序的。第 j 個特徵值對應於第 j 個特徵向量。

注意

來源 [1], [2]，並特別感謝 Svetlin Penkov 的原創教程。

原始碼

C++

• 可下載程式碼：點選此處
• 程式碼速覽

   
  #include "opencv2/core.hpp"
  #include "opencv2/imgproc.hpp"
  #include "opencv2/highgui.hpp"
  #include <iostream>
   
  using namespace std;
  using namespace cv;
   
  // 函式宣告
  void drawAxis(Mat&, Point, Point, Scalar, const float);
  double getOrientation(const vector<Point> &, Mat&);
   
  void drawAxis(Mat& img, Point p, Point q, Scalar colour, const float scale = 0.2)
  {
      double angle = atan2( (double) p.y - q.y, (double) p.x - q.x ); // 角度（弧度）
      double hypotenuse = sqrt( (double) (p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
   
      // 這裡我們將箭頭長度縮放 scale 倍
  q.x = (int) (p.x - scale * hypotenuse * cos(angle));
  q.y = (int) (p.y - scale * hypotenuse * sin(angle));
  line(img, p, q, colour, 1, LINE_AA);
   
      // 建立箭頭鉤
  p.x = (int) (q.x + 9 * cos(angle + CV_PI / 4));
  p.y = (int) (q.y + 9 * sin(angle + CV_PI / 4));
  line(img, p, q, colour, 1, LINE_AA);
   
  p.x = (int) (q.x + 9 * cos(angle - CV_PI / 4));
  p.y = (int) (q.y + 9 * sin(angle - CV_PI / 4));
  line(img, p, q, colour, 1, LINE_AA);
  }
   
  double getOrientation(const vector<Point> &pts, Mat &img)
  {
      // 構建 PCA 分析使用的緩衝區
      int sz = static_cast<int>(pts.size());
      Mat data_pts = Mat(sz, 2, CV_64F);
      for (int i = 0; i < data_pts.rows; i++)
      {
  data_pts.at<double>(i, 0) = pts[i].x;
  data_pts.at<double>(i, 1) = pts[i].y;
      }
   
      // 執行 PCA 分析
      PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW);
   
      // 儲存物件的中心
      Point cntr = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)),
                        static_cast<int>(pca_analysis.mean.at<double>(0, 1)));
   
      // 儲存特徵值和特徵向量
  vector<Point2d> eigen_vecs(2);
  vector<double> eigen_val(2);
      for (int i = 0; i < 2; i++)
      {
  eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
  pca_analysis.eigenvectors.at<double>(i, 1));
   
  eigen_val[i] = pca_analysis.eigenvalues.at<double>(i);
      }
   
      // 繪製主成分
  circle(img, cntr, 3, Scalar(255, 0, 255), 2);
      Point p1 = cntr + 0.02 * Point(static_cast<int>(eigen_vecs[0].x * eigen_val[0]), static_cast<int>(eigen_vecs[0].y * eigen_val[0]));
      Point p2 = cntr - 0.02 * Point(static_cast<int>(eigen_vecs[1].x * eigen_val[1]), static_cast<int>(eigen_vecs[1].y * eigen_val[1]));
  drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1);
  drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5);
   
      double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // 方向（弧度）
   
      return angle;
  }
   
  int main(int argc, char** argv)
  {
      // 載入影像
      CommandLineParser parser(argc, argv, "{@input | pca_test1.jpg | input image}");
  parser.about( "此程式演示瞭如何使用 OpenCV PCA 提取物件的方向。\n" );
  parser.printMessage();
   
      Mat src = imread( samples::findFile( parser.get<String>("@input") ) );
   
      // 檢查影像是否成功載入
      if(src.empty())
      {
  cout << "Problem loading image!!!" << endl;
          return EXIT_FAILURE;
      }
   
      imshow("src", src);
   
      // 將影像轉換為灰度影像
      Mat gray;
      cvtColor(src, gray, COLOR_BGR2GRAY);
   
      // 將影像轉換為二值影像
      Mat bw;
      threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);
   
      // 查詢閾值影像中的所有輪廓
  vector<vector<Point> > contours;
      findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);
   
      for (size_t i = 0; i < contours.size(); i++)
      {
          // 計算每個輪廓的面積
          double area = contourArea(contours[i]);
          // 忽略太小或太大的輪廓
          if (area < 1e2 || 1e5 < area) continue;
   
          // 僅為了視覺化目的繪製每個輪廓
          drawContours(src, contours, static_cast<int>(i), Scalar(0, 0, 255), 2);
          // 查詢每個形狀的方向
  getOrientation(contours[i], src);
      }
   
      imshow("output", src);
   
      waitKey();
      return EXIT_SUCCESS;
  }

Java

• 可下載程式碼：點選此處
• 程式碼速覽

  import java.util.ArrayList;
  import java.util.List;
   
  import org.opencv.core.Core;
  import org.opencv.core.CvType;
  import org.opencv.core.Mat;
  import org.opencv.core.MatOfPoint;
  import org.opencv.core.Point;
  import org.opencv.core.Scalar;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgcodecs.Imgcodecs;
  import org.opencv.imgproc.Imgproc;
   
  //此程式演示瞭如何使用 OpenCV PCA 提取物件的方向。
  class IntroductionToPCA {
      private void drawAxis(Mat img, Point p_, Point q_, Scalar colour, float scale) {
  Point p = new Point(p_.x, p_.y);
  Point q = new Point(q_.x, q_.y);
          double angle = Math.atan2(p.y - q.y, p.x - q.x); // 角度（弧度）
          double hypotenuse = Math.sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
   
          // 這裡我們將箭頭長度縮放 scale 倍
  q.x = (int) (p.x - scale * hypotenuse * Math.cos(angle));
  q.y = (int) (p.y - scale * hypotenuse * Math.sin(angle));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
   
          // 建立箭頭鉤
  p.x = (int) (q.x + 9 * Math.cos(angle + Math.PI / 4));
  p.y = (int) (q.y + 9 * Math.sin(angle + Math.PI / 4));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
   
  p.x = (int) (q.x + 9 * Math.cos(angle - Math.PI / 4));
  p.y = (int) (q.y + 9 * Math.sin(angle - Math.PI / 4));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
      }
   
      private double getOrientation(MatOfPoint ptsMat, Mat img) {
  List<Point> pts = ptsMat.toList();
          // Construct a buffer used by the pca analysis
          int sz = pts.size();
  Mat dataPts = new Mat(sz, 2, CvType.CV_64F);
          double[] dataPtsData = new double[(int) (dataPts.total() * dataPts.channels())];
          for (int i = 0; i < dataPts.rows(); i++) {
  dataPtsData[i * dataPts.cols()] = pts.get(i).x;
  dataPtsData[i * dataPts.cols() + 1] = pts.get(i).y;
          }
  dataPts.put(0, 0, dataPtsData);
   
          // 執行 PCA 分析
  Mat mean = new Mat();
  Mat eigenvectors = new Mat();
  Mat eigenvalues = new Mat();
  Core.PCACompute2(dataPts, mean, eigenvectors, eigenvalues);
          double[] meanData = new double[(int) (mean.total() * mean.channels())];
  mean.get(0, 0, meanData);
   
          // Store the center of the object
  Point cntr = new Point(meanData[0], meanData[1]);
   
          // Store the eigenvalues and eigenvectors
          double[] eigenvectorsData = new double[(int) (eigenvectors.total() * eigenvectors.channels())];
          double[] eigenvaluesData = new double[(int) (eigenvalues.total() * eigenvalues.channels())];
  eigenvectors.get(0, 0, eigenvectorsData);
  eigenvalues.get(0, 0, eigenvaluesData);
   
          // 繪製主成分
  Imgproc.circle(img, cntr, 3, new Scalar(255, 0, 255), 2);
  Point p1 = new Point(cntr.x + 0.02 * eigenvectorsData[0] * eigenvaluesData[0],
  cntr.y + 0.02 * eigenvectorsData[1] * eigenvaluesData[0]);
  Point p2 = new Point(cntr.x - 0.02 * eigenvectorsData[2] * eigenvaluesData[1],
  cntr.y - 0.02 * eigenvectorsData[3] * eigenvaluesData[1]);
  drawAxis(img, cntr, p1, new Scalar(0, 255, 0), 1);
  drawAxis(img, cntr, p2, new Scalar(255, 255, 0), 5);
   
          double angle = Math.atan2(eigenvectorsData[1], eigenvectorsData[0]); // 方向（弧度）
   
          return angle;
      }
   
      public void run(String[] args) {
          // 載入影像
  String filename = args.length > 0 ? args[0] : "../data/pca_test1.jpg";
  Mat src = Imgcodecs.imread(filename);
   
          // 檢查影像是否成功載入
          if (src.empty()) {
  System.err.println("無法讀取影像: " + filename);
  System.exit(0);
          }
   
  Mat srcOriginal = src.clone();
  HighGui.imshow("src", srcOriginal);
   
          // 將影像轉換為灰度影像
  Mat gray = new Mat();
  Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
   
          // 將影像轉換為二值影像
  Mat bw = new Mat();
  Imgproc.threshold(gray, bw, 50, 255, Imgproc.THRESH_BINARY | Imgproc.THRESH_OTSU);
   
          // 查詢閾值影像中的所有輪廓
  List<MatOfPoint> contours = new ArrayList<>();
  Mat hierarchy = new Mat();
  Imgproc.findContours(bw, contours, hierarchy, Imgproc.RETR_LIST, Imgproc.CHAIN_APPROX_NONE);
   
          for (int i = 0; i < contours.size(); i++) {
              // 計算每個輪廓的面積
              double area = Imgproc.contourArea(contours.get(i));
              // 忽略太小或太大的輪廓
              if (area < 1e2 || 1e5 < area)
                  continue;
   
              // 僅為了視覺化目的繪製每個輪廓
  Imgproc.drawContours(src, contours, i, new Scalar(0, 0, 255), 2);
              // 查詢每個形狀的方向
  getOrientation(contours.get(i), src);
          }
   
  HighGui.imshow("output", src);
   
  HighGui.waitKey();
  System.exit(0);
      }
  }
   
  public class IntroductionToPCADemo {
      public static void main(String[] args) {
          // 載入本地 OpenCV 庫
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
   
          new IntroductionToPCA().run(args);
      }
  }

Python

• 可下載程式碼：點選此處
• 程式碼速覽

  from __future__ import print_function
  from __future__ import division
  import cv2 as cv
  import numpy as np
  import argparse
  from math import atan2, cos, sin, sqrt, pi
   
  def drawAxis(img, p_, q_, colour, scale)
  p = list(p_)
  q = list(q_)
      
  angle = atan2(p[1] - q[1], p[0] - q[0]) # 角度（弧度）
  hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
   
      # 在此處我們將箭頭按比例因子加長
  q[0] = p[0] - scale * hypotenuse * cos(angle)
  q[1] = p[1] - scale * hypotenuse * sin(angle)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
   
      # 建立箭頭倒鉤
  p[0] = q[0] + 9 * cos(angle + pi / 4)
  p[1] = q[1] + 9 * sin(angle + pi / 4)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
   
  p[0] = q[0] + 9 * cos(angle - pi / 4)
  p[1] = q[1] + 9 * sin(angle - pi / 4)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
      
   
  def getOrientation(pts, img)
      
  sz = len(pts)
  data_pts = np.empty((sz, 2), dtype=np.float64)
      for i in range(data_pts.shape[0])
  data_pts[i,0] = pts[i,0,0]
  data_pts[i,1] = pts[i,0,1]
   
      # 執行 PCA 分析
  mean = np.empty((0))
  mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)
   
      # Store the center of the object
  cntr = (int(mean[0,0]), int(mean[0,1]))
      
   
      
      cv.circle(img, cntr, 3, (255, 0, 255), 2)
  p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
  p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
  drawAxis(img, cntr, p1, (0, 255, 0), 1)
  drawAxis(img, cntr, p2, (255, 255, 0), 5)
   
  angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # 方向（弧度）
      
   
      return angle
   
   
  parser = argparse.ArgumentParser(description='主成分分析 (PCA) 教程程式碼。\
  本程式演示如何使用 OpenCV PCA 提取物件的方向。')
  parser.add_argument('--input', help='輸入影像的路徑。', default='pca_test1.jpg')
  args = parser.parse_args()
   
  src = cv.imread(cv.samples.findFile(args.input))
  # 檢查影像是否成功載入
  if src is None
  print('無法開啟或找到影像：', args.input)
  exit(0)
   
  cv.imshow('src', src)
   
  # 將影像轉換為灰度圖
  gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
   
  # 將影像轉換為二值圖
  _, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)
   
   
   
  contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
   
  for i, c in enumerate(contours)
      # 計算每個輪廓的面積
  area = cv.contourArea(c)
      # 忽略過小或過大的輪廓
      if area < 1e2 or 1e5 < area
          continue
   
      # 僅為視覺化目的繪製每個輪廓
      cv.drawContours(src, contours, i, (0, 0, 255), 2)
      # 查詢每個形狀的方向
  getOrientation(c, src)
   
   
  cv.imshow('output', src)
  cv.waitKey()

注意

另一個使用 PCA 進行降維並保持一定方差的示例可以在 opencv_source_code/samples/cpp/pca.cpp 找到。

解釋

• 讀取影像並將其轉換為二值圖

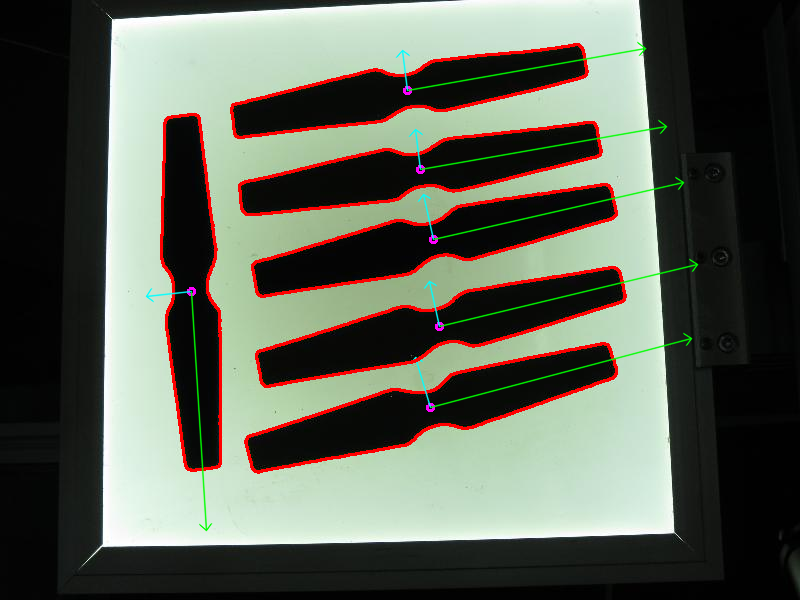
在這裡，我們應用必要的預處理程式，以便能夠檢測感興趣的物件。

C++

    // 載入影像
    CommandLineParser parser(argc, argv, "{@input | pca_test1.jpg | input image}");
parser.about( "此程式演示瞭如何使用 OpenCV PCA 提取物件的方向。\n" );
parser.printMessage();
 
    Mat src = imread( samples::findFile( parser.get<String>("@input") ) );
 
    // 檢查影像是否成功載入
    if(src.empty())
    {
cout << "Problem loading image!!!" << endl;
        return EXIT_FAILURE;
    }
 
    imshow("src", src);
 
    // 將影像轉換為灰度影像
    Mat gray;
    cvtColor(src, gray, COLOR_BGR2GRAY);
 
    // 將影像轉換為二值影像
    Mat bw;
    threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);

Java

        // 載入影像
        String filename = args.length > 0 ? args[0] : "../data/pca_test1.jpg";
Mat src = Imgcodecs.imread(filename);
 
        // 檢查影像是否成功載入
        if (src.empty()) {
System.err.println("無法讀取影像: " + filename);
System.exit(0);
        }
 
Mat srcOriginal = src.clone();
HighGui.imshow("src", srcOriginal);
 
        // 將影像轉換為灰度影像
Mat gray = new Mat();
Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
 
        // 將影像轉換為二值影像
Mat bw = new Mat();
Imgproc.threshold(gray, bw, 50, 255, Imgproc.THRESH_BINARY | Imgproc.THRESH_OTSU);

Python

parser = argparse.ArgumentParser(description='主成分分析 (PCA) 教程程式碼。\
本程式演示如何使用 OpenCV PCA 提取物件的方向。')
parser.add_argument('--input', help='輸入影像的路徑。', default='pca_test1.jpg')
args = parser.parse_args()
 
src = cv.imread(cv.samples.findFile(args.input))
# 檢查影像是否成功載入
if src is None
print('無法開啟或找到影像：', args.input)
exit(0)
 
cv.imshow('src', src)
 
# 將影像轉換為灰度圖
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
 
# 將影像轉換為二值圖
_, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)

• 提取感興趣的物件

然後透過大小查詢和過濾輪廓，並獲取剩餘輪廓的方向。

C++

    // 查詢閾值影像中的所有輪廓
vector<vector<Point> > contours;
    findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);
 
    for (size_t i = 0; i < contours.size(); i++)
    {
        // 計算每個輪廓的面積
        double area = contourArea(contours[i]);
        // 忽略太小或太大的輪廓
        if (area < 1e2 || 1e5 < area) continue;
 
        // 僅為了視覺化目的繪製每個輪廓
        drawContours(src, contours, static_cast<int>(i), Scalar(0, 0, 255), 2);
        // 查詢每個形狀的方向
getOrientation(contours[i], src);
    }

Java

        // 查詢閾值影像中的所有輪廓
List<MatOfPoint> contours = new ArrayList<>();
Mat hierarchy = new Mat();
Imgproc.findContours(bw, contours, hierarchy, Imgproc.RETR_LIST, Imgproc.CHAIN_APPROX_NONE);
 
        for (int i = 0; i < contours.size(); i++) {
            // 計算每個輪廓的面積
            double area = Imgproc.contourArea(contours.get(i));
            // 忽略太小或太大的輪廓
            if (area < 1e2 || 1e5 < area)
                continue;
 
            // 僅為了視覺化目的繪製每個輪廓
Imgproc.drawContours(src, contours, i, new Scalar(0, 0, 255), 2);
            // 查詢每個形狀的方向
getOrientation(contours.get(i), src);
        }

Python

contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
 
for i, c in enumerate(contours)
    # 計算每個輪廓的面積
area = cv.contourArea(c)
    # 忽略過小或過大的輪廓
    if area < 1e2 or 1e5 < area
        continue
 
    # 僅為視覺化目的繪製每個輪廓
    cv.drawContours(src, contours, i, (0, 0, 255), 2)
    # 查詢每個形狀的方向
getOrientation(c, src)

• 提取方向

透過呼叫 getOrientation() 函式來提取方向，該函式執行所有 PCA 過程。

C++

    // 構建 PCA 分析使用的緩衝區
    int sz = static_cast<int>(pts.size());
    Mat data_pts = Mat(sz, 2, CV_64F);
    for (int i = 0; i < data_pts.rows; i++)
    {
data_pts.at<double>(i, 0) = pts[i].x;
data_pts.at<double>(i, 1) = pts[i].y;
    }
 
    // 執行 PCA 分析
    PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW);
 
    // 儲存物件的中心
    Point cntr = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)),
                      static_cast<int>(pca_analysis.mean.at<double>(0, 1)));
 
    // 儲存特徵值和特徵向量
vector<Point2d> eigen_vecs(2);
vector<double> eigen_val(2);
    for (int i = 0; i < 2; i++)
    {
eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
pca_analysis.eigenvectors.at<double>(i, 1));
 
eigen_val[i] = pca_analysis.eigenvalues.at<double>(i);
    }

Java

        // Construct a buffer used by the pca analysis
        int sz = pts.size();
Mat dataPts = new Mat(sz, 2, CvType.CV_64F);
        double[] dataPtsData = new double[(int) (dataPts.total() * dataPts.channels())];
        for (int i = 0; i < dataPts.rows(); i++) {
dataPtsData[i * dataPts.cols()] = pts.get(i).x;
dataPtsData[i * dataPts.cols() + 1] = pts.get(i).y;
        }
dataPts.put(0, 0, dataPtsData);
 
        // 執行 PCA 分析
Mat mean = new Mat();
Mat eigenvectors = new Mat();
Mat eigenvalues = new Mat();
Core.PCACompute2(dataPts, mean, eigenvectors, eigenvalues);
        double[] meanData = new double[(int) (mean.total() * mean.channels())];
        mean.get(0, 0, meanData);
 
        // Store the center of the object
        Point cntr = new Point(meanData[0], meanData[1]);
 
        // Store the eigenvalues and eigenvectors
        double[] eigenvectorsData = new double[(int) (eigenvectors.total() * eigenvectors.channels())];
        double[] eigenvaluesData = new double[(int) (eigenvalues.total() * eigenvalues.channels())];
eigenvectors.get(0, 0, eigenvectorsData);
eigenvalues.get(0, 0, eigenvaluesData);

Python

sz = len(pts)
data_pts = np.empty((sz, 2), dtype=np.float64)
    for i in range(data_pts.shape[0])
data_pts[i,0] = pts[i,0,0]
data_pts[i,1] = pts[i,0,1]
 
    # 執行 PCA 分析
mean = np.empty((0))
mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)
 
    # Store the center of the object
cntr = (int(mean[0,0]), int(mean[0,1]))

首先，資料需要排列成大小為 n x 2 的矩陣，其中 n 是我們擁有的資料點數量。然後我們可以執行 PCA 分析。計算出的均值（即質心）儲存在 cntr 變數中，特徵向量和特徵值儲存在相應的 std::vector 中。

• 視覺化結果

最終結果透過 drawAxis() 函式視覺化，其中主成分以線條繪製，每個特徵向量乘以其特徵值並平移到均值位置。

C++

    // 繪製主成分
    circle(img, cntr, 3, Scalar(255, 0, 255), 2);
    Point p1 = cntr + 0.02 * Point(static_cast<int>(eigen_vecs[0].x * eigen_val[0]), static_cast<int>(eigen_vecs[0].y * eigen_val[0]));
    Point p2 = cntr - 0.02 * Point(static_cast<int>(eigen_vecs[1].x * eigen_val[1]), static_cast<int>(eigen_vecs[1].y * eigen_val[1]));
drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1);
drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5);
 
    double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // 方向（弧度）

Java

        // 繪製主成分
Imgproc.circle(img, cntr, 3, new Scalar(255, 0, 255), 2);
        Point p1 = new Point(cntr.x + 0.02 * eigenvectorsData[0] * eigenvaluesData[0],
cntr.y + 0.02 * eigenvectorsData[1] * eigenvaluesData[0]);
        Point p2 = new Point(cntr.x - 0.02 * eigenvectorsData[2] * eigenvaluesData[1],
cntr.y - 0.02 * eigenvectorsData[3] * eigenvaluesData[1]);
drawAxis(img, cntr, p1, new Scalar(0, 255, 0), 1);
drawAxis(img, cntr, p2, new Scalar(255, 255, 0), 5);
 
        double angle = Math.atan2(eigenvectorsData[1], eigenvectorsData[0]); // 方向（弧度）

Python

    cv.circle(img, cntr, 3, (255, 0, 255), 2)
p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
drawAxis(img, cntr, p1, (0, 255, 0), 1)
drawAxis(img, cntr, p2, (255, 255, 0), 5)
 
angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # 方向（弧度）

C++

    double angle = atan2( (double) p.y - q.y, (double) p.x - q.x ); // 角度（弧度）
    double hypotenuse = sqrt( (double) (p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
 
    // 這裡我們將箭頭長度縮放 scale 倍
q.x = (int) (p.x - scale * hypotenuse * cos(angle));
q.y = (int) (p.y - scale * hypotenuse * sin(angle));
    line(img, p, q, colour, 1, LINE_AA);
 
    // 建立箭頭鉤
p.x = (int) (q.x + 9 * cos(angle + CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle + CV_PI / 4));
    line(img, p, q, colour, 1, LINE_AA);
 
p.x = (int) (q.x + 9 * cos(angle - CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle - CV_PI / 4));
    line(img, p, q, colour, 1, LINE_AA);

Java

        double angle = Math.atan2(p.y - q.y, p.x - q.x); // 角度（弧度）
        double hypotenuse = Math.sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
 
        // 這裡我們將箭頭長度縮放 scale 倍
q.x = (int) (p.x - scale * hypotenuse * Math.cos(angle));
q.y = (int) (p.y - scale * hypotenuse * Math.sin(angle));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
 
        // 建立箭頭鉤
p.x = (int) (q.x + 9 * Math.cos(angle + Math.PI / 4));
p.y = (int) (q.y + 9 * Math.sin(angle + Math.PI / 4));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
 
p.x = (int) (q.x + 9 * Math.cos(angle - Math.PI / 4));
p.y = (int) (q.y + 9 * Math.sin(angle - Math.PI / 4));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);

Python

angle = atan2(p[1] - q[1], p[0] - q[0]) # 角度（弧度）
hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
 
    # 在此處我們將箭頭按比例因子加長
q[0] = p[0] - scale * hypotenuse * cos(angle)
q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
 
    # 建立箭頭倒鉤
p[0] = q[0] + 9 * cos(angle + pi / 4)
p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
 
p[0] = q[0] + 9 * cos(angle - pi / 4)
p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)

結果

該程式碼開啟一幅影像，查詢檢測到的感興趣物件的方向，然後透過繪製檢測到的感興趣物件的輪廓、中心點以及與提取方向相關的 x 軸和 y 軸來視覺化結果。