 |
OpenCV 4.12.0
開源計算機視覺
|
 |
OpenCV 4.12.0
開源計算機視覺
|
在機器學習演算法中,存在訓練資料的概念。訓練資料包括幾個組成部分
如您所見,訓練資料可能具有相當複雜的結構;此外,它可能非常大和/或並非完全可用,因此需要對此概念進行抽象。在 OpenCV ml 中,為此有一個 cv::ml::TrainData 類。
這種簡單的分類模型假設每個類別的特徵向量都呈正態分佈(儘管不一定是獨立分佈的)。因此,整個資料分佈函式被假定為高斯混合模型,每個類別一個分量。該演算法利用訓練資料估計每個類別的均值向量和協方差矩陣,然後使用它們進行預測。
該演算法快取所有訓練樣本,並透過分析樣本的特定數量(K)最近鄰居,使用投票、計算加權和等方式來預測新樣本的響應。該方法有時被稱為“透過示例學習”,因為在預測時,它會尋找具有已知響應且最接近給定向量的特徵向量。
最初,支援向量機(SVM)是一種構建最優二元(2類)分類器的技術。後來,該技術擴充套件到迴歸和聚類問題。SVM是基於核方法的特例。它使用核函式將特徵向量對映到更高維空間,並在此空間中構建最優線性判別函式或與訓練資料擬合的最優超平面。在SVM的情況下,核函式沒有明確定義。相反,需要定義超空間中任意2點之間的距離。
該解決方案是最優的,這意味著分離超平面與來自兩個類(在2類分類器的情況下)的最近特徵向量之間的間隔最大。最接近超平面的特徵向量被稱為支援向量,這意味著其他向量的位置不影響超平面(決策函式)。
OpenCV 中的 SVM 實現基於 [51]
應使用 StatModel::predict(samples, results, flags)。傳遞 flags=StatModel::RAW_OUTPUT 以獲取 SVM 的原始響應(在迴歸、1類或2類分類問題中)。
本節討論的 ML 類實現了 [41] 中描述的分類與迴歸樹演算法。
類 cv::ml::DTrees 表示單個決策樹或決策樹的集合。它也是 RTrees 和 Boost 的基類。
決策樹是一種二叉樹(每個非葉節點有兩個子節點的樹)。它既可以用於分類,也可以用於迴歸。對於分類,每個樹葉都標有類別標籤;多個葉子可以具有相同的標籤。對於迴歸,每個樹葉也被賦一個常數,因此近似函式是分段常數。
為了到達葉節點並獲得輸入特徵向量的響應,預測過程從根節點開始。從每個非葉節點,過程根據儲存在觀察節點中的某個變數的值,向左(選擇左子節點作為下一個觀察節點)或向右。可能的變數如下:
因此,在每個節點中,使用一對實體(variable_index,決策規則(閾值/子集))。這對實體被稱為一個分裂(基於變數variable_index進行分裂)。一旦到達葉節點,賦給該節點的值將用作預測過程的輸出。
有時,輸入向量的某些特徵可能會丟失(例如,在黑暗中很難確定物體顏色),預測過程可能會卡在某個節點上(在上述示例中,如果節點按顏色劃分)。為了避免這種情況,決策樹使用所謂的代理分裂。也就是說,除了最佳的“主要”分裂之外,每個樹節點還可以根據一個或多個其他變數進行分裂,這些變數會產生幾乎相同的結果。
樹是從根節點開始遞迴構建的。所有訓練資料(特徵向量和響應)都用於分裂根節點。在每個節點中,根據某些標準找到最優決策規則(最佳“主要”分裂)。在機器學習中,分類使用基尼“純度”標準,迴歸使用平方誤差和。然後,如有必要,找到代理分裂。它們類似於訓練資料上的主要分裂結果。所有資料都使用主要分裂和代理分裂(就像在預測過程中所做的那樣)在左、右子節點之間進行劃分。然後,該過程遞迴地分裂左右節點。在每個節點,遞迴過程可以在以下任一情況下停止(即停止進一步分裂節點):
當樹構建完成後,如有必要,可以使用交叉驗證程式對其進行剪枝。也就是說,可能導致模型過擬合的某些樹分支會被剪除。通常,此過程僅應用於獨立的決策樹。樹整合模型通常會構建足夠小的樹,並使用其自身的保護機制來防止過擬合。
除了作為決策樹的明顯用途的預測之外,決策樹還可以用於各種資料分析。構建的決策樹演算法的關鍵特性之一是能夠計算每個變數的重要性(相對決定能力)。例如,在垃圾郵件過濾器中,如果使用訊息中出現的詞彙集合作為特徵向量,則變數重要性評級可用於確定最“指示垃圾郵件”的詞彙,從而有助於保持字典大小合理。
每個變數的重要性是根據樹中該變數的所有分裂(主要分裂和代理分裂)計算的。因此,為了正確計算變數重要性,即使沒有缺失資料,也必須在訓練引數中啟用代理分裂。
常見的機器學習任務是監督學習。在監督學習中,目標是學習輸入 \(x\) 和輸出 \(y\) 之間的函式關係 \(F: y = F(x)\) 。預測定性輸出稱為分類,而預測定量輸出稱為迴歸。
提升法是一個強大的學習概念,為監督分類學習任務提供瞭解決方案。它結合了許多“弱”分類器的效能,以產生一個強大的委員會 [276]。弱分類器只要求比隨機猜測好,因此可以非常簡單且計算成本低。然而,許多弱分類器能夠巧妙地組合結果,形成一個強大的分類器,其效能通常優於大多數“單體”強分類器,如 SVM 和神經網路。
決策樹是提升法方案中最常用的弱分類器。通常,每棵樹只有一個分裂節點的最簡單決策樹(稱為“樹樁”)就足夠了。
提升模型基於 \(N\) 個訓練樣本 \({(x_i,y_i)}1N\) ,其中 \(x_i \in{R^K}\) 且 \(y_i \in{-1, +1}\) 。 \(x_i\) 是一個 \(K\) 維向量。每個分量編碼與當前學習任務相關的特徵。所需的二分類輸出編碼為 -1 和 +1。
提升法的不同變體包括離散 Adaboost、實值 AdaBoost、LogitBoost 和 Gentle AdaBoost [97]。它們在總體結構上都非常相似。因此,本章僅關注下面概述的標準兩類離散 AdaBoost 演算法。最初為每個樣本分配相同的權重(步驟 2)。然後,在加權訓練資料上訓練一個弱分類器 \(f_{m(x)}\) (步驟 3a)。計算其加權訓練誤差和縮放因子 \(c_m\) (步驟 3b)。對被錯誤分類的訓練樣本增加權重(步驟 3c)。然後對所有權重進行歸一化,尋找下一個弱分類器的過程繼續進行 \(M\) -1 次。最終分類器 \(F(x)\) 是各個弱分類器加權和的符號(步驟 4)。
兩類離散 AdaBoost 演算法
為了減少提升模型的計算時間,同時不顯著降低精度,可以使用影響修剪技術。隨著訓練演算法的進行和整合中樹的數量增加,更多的訓練樣本被正確分類並具有更高的置信度,因此這些樣本在後續迭代中獲得較小的權重。相對權重非常低的示例對弱分類器訓練的影響很小。因此,在弱分類器訓練期間可以排除這些示例,而不會對生成的分類器產生太大影響。此過程由 weight_trim_rate 引數控制。在弱分類器訓練中,僅使用總權重質量中總結分數 weight_trim_rate 的示例。請注意,所有訓練示例的權重在每次訓練迭代時都會重新計算。在特定迭代中刪除的示例可以在後續學習某些弱分類器時再次使用 [97]
應使用 StatModel::predict(samples, results, flags)。傳遞 flags=StatModel::RAW_OUTPUT 以獲取 Boost 分類器的原始和。
隨機樹由 Leo Breiman 和 Adele Cutler 引入:http://www.stat.berkeley.edu/users/breiman/RandomForests/。該演算法可以處理分類和迴歸問題。隨機樹是樹預測器的一個集合(整合),在本節中稱為森林(該術語也由 L. Breiman 引入)。分類工作方式如下:隨機樹分類器接收輸入特徵向量,使用森林中的每棵樹對其進行分類,並輸出獲得多數“投票”的類別標籤。在迴歸的情況下,分類器響應是森林中所有樹的響應平均值。
所有樹都使用相同的引數進行訓練,但訓練集不同。這些集合是使用自助法(bootstrap)從原始訓練集生成的:對於每個訓練集,您隨機選擇與原始集合相同數量的向量(=N)。向量是帶替換抽樣的。也就是說,某些向量會出現多次,而某些向量會缺失。在每棵訓練樹的每個節點,並非所有變數都用於尋找最佳分裂,而是使用它們的隨機子集。每個節點都會生成一個新的子集。但是,其大小對於所有節點和所有樹都是固定的。它是一個訓練引數,預設設定為 \(\sqrt{變數數量}\) 。所有構建的樹都不會被剪枝。
在隨機樹中,無需任何精度估計程式,例如交叉驗證或自助法,也無需單獨的測試集來估計訓練誤差。誤差在訓練期間內部估計。當透過有放回抽樣抽取當前樹的訓練集時,會留下一些向量(即所謂的袋外(oob)資料)。oob 資料的大小約為 N/3。分類誤差透過以下方式使用此 oob 資料進行估計:
有關隨機樹的使用示例,請參閱 OpenCV 發行版中的 letter_recog.cpp 示例。
參考文獻
期望最大化(EM)演算法估計具有指定混合數量的高斯混合分佈形式的多元機率密度函式引數。
考慮從高斯混合分佈中抽取的 d 維歐幾里得空間中的 N 個特徵向量集合 { \(x_1, x_2,...,x_{N}\) }
\[p(x;a_k,S_k, \pi _k) = \sum _{k=1}^{m} \pi _kp_k(x), \quad \pi _k \geq 0, \quad \sum _{k=1}^{m} \pi _k=1,\]
\[p_k(x)= \varphi (x;a_k,S_k)= \frac{1}{(2\pi)^{d/2}\mid{S_k}\mid^{1/2}} exp \left \{ - \frac{1}{2} (x-a_k)^TS_k^{-1}(x-a_k) \right \} ,\]
其中 \(m\) 是混合數,\(p_k\) 是均值為 \(a_k\) 且協方差矩陣為 \(S_k\) 的正態分佈密度,\(\pi_k\) 是第 k 個混合的權重。給定混合數 \(M\) 和樣本 \(x_i\), \(i=1..N\),演算法尋找所有混合引數 \(a_k\), \(S_k\) 和 \(\pi_k\) 的最大似然估計(MLE)
\[L(x, \theta )=logp(x, \theta )= \sum _{i=1}^{N}log \left ( \sum _{k=1}^{m} \pi _kp_k(x) \right ) \to \max _{ \theta \in \Theta },\]
\[\Theta = \left \{ (a_k,S_k, \pi _k): a_k \in \mathbbm{R} ^d,S_k=S_k^T>0,S_k \in \mathbbm{R} ^{d \times d}, \pi _k \geq 0, \sum _{k=1}^{m} \pi _k=1 \right \} .\]
EM 演算法是一個迭代過程。每次迭代包括兩個步驟。在第一步(期望步或 E 步)中,您使用當前可用的混合引數估計值找到樣本 i 屬於混合 k 的機率 \(p_{i,k}\) (在下面的公式中表示為 \(\alpha_{i,k}\) )
\[\alpha _{ki} = \frac{\pi_k\varphi(x;a_k,S_k)}{\sum\limits_{j=1}^{m}\pi_j\varphi(x;a_j,S_j)} .\]
在第二步(最大化步或 M 步)中,使用計算出的機率來細化混合引數估計值
\[\pi _k= \frac{1}{N} \sum _{i=1}^{N} \alpha _{ki}, \quad a_k= \frac{\sum\limits_{i=1}^{N}\alpha_{ki}x_i}{\sum\limits_{i=1}^{N}\alpha_{ki}} , \quad S_k= \frac{\sum\limits_{i=1}^{N}\alpha_{ki}(x_i-a_k)(x_i-a_k)^T}{\sum\limits_{i=1}^{N}\alpha_{ki}}\]
或者,當可以提供 \(p_{i,k}\) 的初始值時,演算法可以從 M 步開始。當 \(p_{i,k}\) 未知時的另一種替代方法是使用更簡單的聚類演算法對輸入樣本進行預聚類,從而獲得初始 \(p_{i,k}\) 。通常(包括機器學習),k-means 演算法用於此目的。
EM 演算法的主要問題之一是要估計的引數數量龐大。大多數引數存在於協方差矩陣中,每個協方差矩陣都是 \(d \times d\) 個元素,其中 \(d\) 是特徵空間的維度。然而,在許多實際問題中,協方差矩陣接近對角矩陣甚至 \(\mu_k*I\) ,其中 \(I\) 是單位矩陣,\(\mu_k\) 是依賴於混合的“尺度”引數。因此,一個穩健的計算方案可以從對協方差矩陣施加更嚴格的約束開始,然後將估計的引數作為輸入用於約束較少的最佳化問題(通常對角協方差矩陣已經是一個足夠好的近似)。
參考文獻
ML 實現了前饋人工神經網路,或者更具體地說,多層感知器(MLP),這是最常用的神經網路型別。MLP 由輸入層、輸出層和一個或多個隱藏層組成。MLP 的每一層都包含一個或多個神經元,它們與前一層和下一層的神經元定向連線。下面的示例表示一個3層感知器,具有三個輸入、兩個輸出,以及一個包含五個神經元的隱藏層
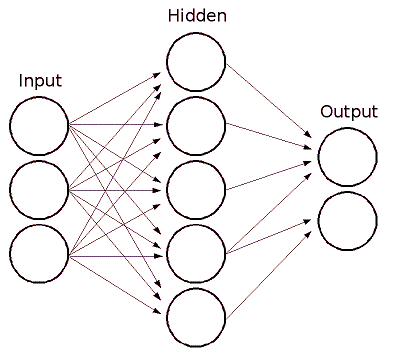
MLP 中的所有神經元都相似。每個神經元都有多個輸入連線(它將前一層中多個神經元的輸出值作為輸入)和多個輸出連線(它將響應傳遞給下一層中的多個神經元)。從前一層檢索到的值會與特定權重(每個神經元獨有)以及偏置項相加。總和透過啟用函式 \(f\) 進行轉換,該函式對於不同神經元也可能不同。
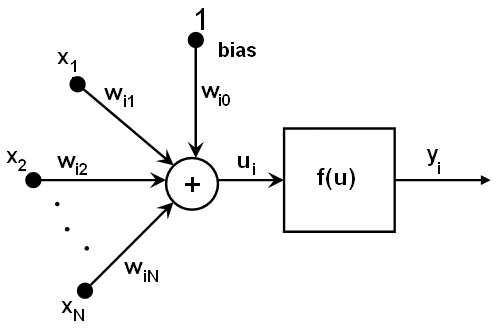
換句話說,給定層 \(n\) 的輸出 \(x_j\) ,層 \(n+1\) 的輸出 \(y_i\) 計算如下:
\[u_i = \sum _j (w^{n+1}_{i,j}*x_j) + w^{n+1}_{i,bias}\]
\[y_i = f(u_i)\]
可以使用不同的啟用函式。ML 實現了三種標準函式
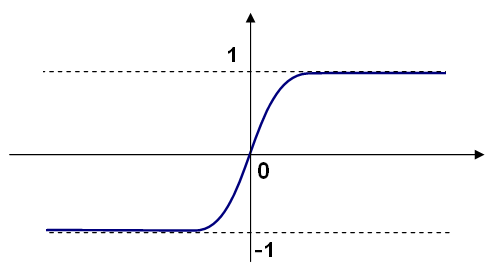
在 ML 中,所有神經元都具有相同的啟用函式,並具有相同的自由引數( \(\alpha, \beta\) ),這些引數由使用者指定且不受訓練演算法更改。
因此,整個訓練好的網路工作方式如下:
因此,要計算網路,您需要知道所有權重 \(w^{n+1)}_{i,j}\) 。權重由訓練演算法計算。該演算法接收一個訓練集,其中包含多個輸入向量及其對應的輸出向量,並迭代調整權重,以使網路能夠對所提供的輸入向量給出期望的響應。
網路規模(隱藏層數量及其大小)越大,潛在的網路靈活性就越大。訓練集上的誤差可以做得任意小。但同時,學習到的網路也會“學習”訓練集中存在的噪聲,因此在網路規模達到一定限制後,測試集上的誤差通常會開始增加。此外,大型網路的訓練時間遠長於小型網路,因此合理的資料預處理是必要的,可以利用 cv::PCA 或類似技術,只在基本特徵上訓練一個較小的網路。
MLP 的另一個特點是無法直接處理分類資料。然而,有一種變通方法。如果輸入或輸出層中的某個特徵(對於 \(n>2\) 的 n 類分類器)是分類的,並且可以取 \(M>2\) 個不同的值,則將其表示為 M 個元素的二元組是有意義的,其中第 i 個元素當且僅當該特徵等於 M 個可能值中的第 i 個值時為 1。這會增加輸入/輸出層的大小,但會加快訓練演算法的收斂速度,同時允許這些變數的“模糊”值,即一組機率而不是固定值。
ML 實現了兩種訓練 MLP 的演算法。第一種演算法是經典的隨機序列反向傳播演算法。第二種(預設)是批次 RPROP 演算法。
ML 實現了邏輯迴歸,這是一種機率分類技術。邏輯迴歸是一種二分類演算法,與支援向量機 (SVM) 密切相關。與 SVM 類似,邏輯迴歸可以擴充套件到處理多類分類問題,例如數字識別(即從給定影像中識別 0、1、2、3 等數字)。此版本的邏輯迴歸支援二分類和多分類(對於多分類,它會建立多個兩類分類器)。為了訓練邏輯迴歸分類器,使用了批次梯度下降和迷你批次梯度下降演算法(參見 http://en.wikipedia.org/wiki/Gradient_descent_optimization)。邏輯迴歸是一種判別式分類器(更多詳情請參見 http://www.cs.cmu.edu/~tom/NewChapters.html)。邏輯迴歸在 LogisticRegression 中作為 C++ 類實現。
在邏輯迴歸中,我們嘗試最佳化訓練引數 \(\theta\) ,以實現假設 \(0 \leq h_\theta(x) \leq 1\) 。我們有 \(h_\theta(x) = g(h_\theta(x))\) 且 \(g(z) = \frac{1}{1+e^{-z}}\) 作為邏輯或 S 形函式。“邏輯迴歸”中的“邏輯”一詞即指此函式。對於給定類別 0 和 1 的二分類問題資料,如果 \(h_\theta(x) \geq 0.5\) 則可以確定給定資料例項屬於類別 1,如果 \(h_\theta(x) < 0.5\) 則屬於類別 0。
在邏輯迴歸中,選擇正確的引數對於減少訓練誤差和確保高訓練精度至關重要
邏輯迴歸分類器的訓練引數示例如下初始化: