位姿計算概述

位姿計算問題 [185] 包括求解旋轉和平移，以最小化來自 3D-2D 點對應的重投影誤差。

solvePnP 和相關函式估計物件位姿，給定一組物件點、它們對應的影像投影，以及相機內參矩陣和畸變係數，如下圖所示（更準確地說，計算機視覺領域的慣例是使相機座標系的 X 軸指向右側，Y 軸向下，Z 軸向前）。

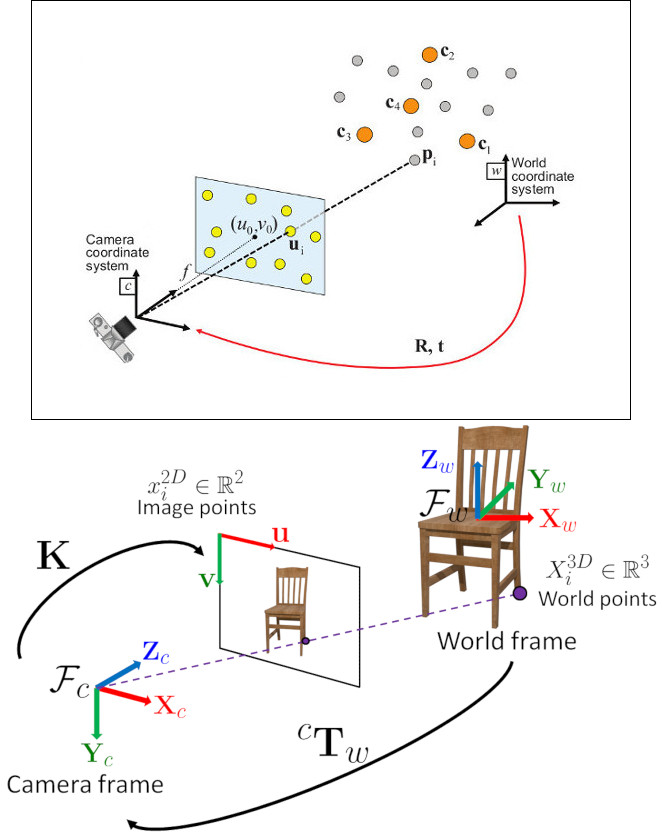
上圖：從 3D-2D 點對應列表計算出的 6 自由度位姿。下圖：考慮的透視投影模型。

在世界座標系 \( \bf{X}_w \) 中表示的點使用透視投影模型 \( \Pi \) 和相機內參矩陣 \( \bf{A} \)（在文獻中也表示為 \( \bf{K} \)）投影到影像平面 \( \left[ u, v \right] \) 中。

\[ \begin{align*} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \bf{A} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

因此，估計的位姿是旋轉向量 (rvec) 和平移向量 (tvec)，它們允許將世界座標系中表示的 3D 點轉換到相機座標系中。

\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

位姿計算方法

請參閱 cv::SolvePnPMethod 列舉文件，瞭解可能值的列表。下面描述了每種方法的一些細節。

cv::SOLVEPNP_ITERATIVE 迭代方法基於 Levenberg-Marquardt 最佳化。在這種情況下，該函式找到一種位姿，使重投影誤差最小化，即觀察到的投影“imagePoints”和投影的（使用 cv::projectPoints ）“objectPoints”之間的平方距離之和。非平面“objectPoints”的初始解至少需要 6 個點，並使用 DLT 演算法。平面“objectPoints”的初始解至少需要 4 個點，並使用單應性分解的位姿。
cv::SOLVEPNP_P3P 該方法基於 X.S. Gao、X.-R. Hou、J. Tang、H.-F. Chang 的論文“透視三點問題的完整解分類”([99])。在這種情況下，該函式恰好需要四個物件點和影像點。
cv::SOLVEPNP_AP3P 該方法基於 T. Ke、S. Roumeliotis 的論文“透視三點問題的有效代數解”([147])。在這種情況下，該函式恰好需要四個物件點和影像點。
cv::SOLVEPNP_EPNP 該方法由 F. Moreno-Noguer、V. Lepetit 和 P. Fua 在論文“EPnP：高效透視 n 點相機位姿估計”([160]) 中引入。
cv::SOLVEPNP_DLS 已損壞的實現。使用此標誌將回退到 EPnP。
該方法基於 J. Hesch 和 S. Roumeliotis 的論文。“PnP 的直接最小二乘 (DLS) 方法”([127])。
cv::SOLVEPNP_UPNP 已損壞的實現。使用此標誌將回退到 EPnP。
該方法基於 A. Penate-Sanchez、J. Andrade-Cetto、F. Moreno-Noguer 的論文。“魯棒相機位姿和焦距估計的窮舉線性化”([217])。在這種情況下，該函式還會估計引數 \(f_x\) 和 \(f_y\)，假設兩者具有相同的值。然後，使用估計的焦距更新 cameraMatrix。
cv::SOLVEPNP_IPPE 該方法基於 T. Collins 和 A. Bartoli 的論文。“無窮小平面到位姿估計”([63])。此方法需要共面對象點。
cv::SOLVEPNP_IPPE_SQUARE 該方法基於 Toby Collins 和 Adrien Bartoli 的論文。“無窮小平面到位姿估計”([63])。此方法適用於標記位姿估計。它需要按以下順序定義的 4 個共面對象點
- 點 0: [-squareLength / 2, squareLength / 2, 0]
- 點 1: [ squareLength / 2, squareLength / 2, 0]
- 點 2: [ squareLength / 2, -squareLength / 2, 0]
- 點 3: [-squareLength / 2, -squareLength / 2, 0]
cv::SOLVEPNP_SQPNP 該方法基於 G. Terzakis 和 M.Lourakis 的論文“透視 n 點問題的一致快速和全域性最優解”([271])。它需要 3 個或更多點。

P3P

cv::solveP3P() 從恰好 3 個 3D-2D 點對應關係計算物件位姿。P3P 問題最多有 4 個解。

注意: 解按重投影誤差排序（從低到高）。

PnP

cv::solvePnP() 返回旋轉向量和平移向量，它們使用不同的方法將物件座標系中表示的 3D 點變換到相機座標系。

P3P 方法 (cv::SOLVEPNP_P3P, cv::SOLVEPNP_AP3P)：需要 4 個輸入點才能返回唯一的解。
cv::SOLVEPNP_IPPE 輸入點必須 >= 4，並且物件點必須共面。
cv::SOLVEPNP_IPPE_SQUARE 適用於標記位姿估計的特殊情況。輸入點的數量必須為 4。物件點必須按以下順序定義
- 點 0: [-squareLength / 2, squareLength / 2, 0]
- 點 1: [ squareLength / 2, squareLength / 2, 0]
- 點 2: [ squareLength / 2, -squareLength / 2, 0]
- 點 3: [-squareLength / 2, -squareLength / 2, 0]
對於所有其他標誌，輸入點的數量必須 >= 4，並且物件點可以是任何配置。

通用 PnP

cv::solvePnPGeneric() 允許檢索所有可能的解。

目前，只有 cv::SOLVEPNP_P3P, cv::SOLVEPNP_AP3P, cv::SOLVEPNP_IPPE, cv::SOLVEPNP_IPPE_SQUARE, cv::SOLVEPNP_SQPNP 可以返回多個解。

RANSAC PnP

cv::solvePnPRansac() 使用 RANSAC 方案計算物件相對於相機座標系的位姿，以處理異常值。

更多資訊可以在 [328] 中找到

位姿細化

位姿細化包括估計旋轉和平移，使用非線性最小化方法並從解的初始估計開始，最小化重投影誤差。OpenCV 提出了 cv::solvePnPRefineLM() 和 cv::solvePnPRefineVVS() 來解決這個問題。

cv::solvePnPRefineLM() 使用非線性 Levenberg-Marquardt 最小化方案 [181] [79]，當前的實現將旋轉更新計算為擾動，而不是在 SO(3) 上計算。

cv::solvePnPRefineVVS() 使用 Gauss-Newton 非線性最小化方案 [185]，並且使用指數對映計算的旋轉部分的更新。

注意: 至少需要三個 3D-2D 點對應關係。