目標

在本教程中，您將學習如何

使用OpenCV函式 cv::warpAffine 實現簡單的重對映例程。
使用OpenCV函式 cv::getRotationMatrix2D 獲取一個 \(2 \times 3\) 旋轉矩陣

理論

什麼是仿射變換？

一種可以透過矩陣乘法（線性變換）然後進行向量加法（平移）來表示的變換。
由上可知，我們可以使用仿射變換來表達
1. 旋轉（線性變換）
2. 平移（向量加法）
3. 縮放操作（線性變換）
您可以看到，仿射變換本質上表示了兩個影像之間的關係。
表示仿射變換的常用方法是使用 \(2 \times 3\) 矩陣。

\[ A = \begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix}_{2 \times 2} B = \begin{bmatrix} b_{00} \\ b_{10} \end{bmatrix}_{2 \times 1} \]

\[ M = \begin{bmatrix} A & B \end{bmatrix} = \begin{bmatrix} a_{00} & a_{01} & b_{00} \\ a_{10} & a_{11} & b_{10} \end{bmatrix}_{2 \times 3} \]

考慮到我們想使用 \(A\) 和 \(B\) 變換一個二維向量 \(X = \begin{bmatrix}x \\ y\end{bmatrix}\)，我們也可以透過以下方式實現：

\(T = A \cdot \begin{bmatrix}x \\ y\end{bmatrix} + B\) 或 \(T = M \cdot [x, y, 1]^{T}\)

\[T = \begin{bmatrix} a_{00}x + a_{01}y + b_{00} \\ a_{10}x + a_{11}y + b_{10} \end{bmatrix}\]

如何獲取仿射變換？

我們提到仿射變換本質上是兩個影像之間的關係。關於這種關係的資訊大致可以透過兩種方式獲得：
1. 我們同時知道 \(X\) 和 \(T\)，並且知道它們之間存在關係。那麼我們的任務就是找到 \(M\)
2. 我們知道 \(M\) 和 \(X\)。要獲取 \(T\)，我們只需要應用 \(T = M \cdot X\)。關於 \(M\) 的資訊可以是顯式的（即擁有 2x3 矩陣），也可以是點之間的幾何關係。
讓我們更好地解釋這一點（b）。由於 \(M\) 關聯兩個影像，我們可以分析最簡單的情況，即它關聯兩個影像中的三個點。請看下圖

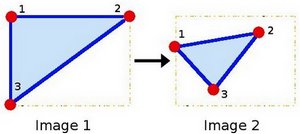
點1、2和3（在影像1中形成一個三角形）被對映到影像2中，仍然形成一個三角形，但現在它們已經發生了顯著變化。如果我們用這3個點找到仿射變換（您可以隨意選擇它們），那麼我們就可以將這種找到的關係應用於影像中的所有畫素。

程式碼

此程式的作用是什麼？
- 載入影像
- 對影像應用仿射變換。此變換是透過三個點之間的關係獲得的。我們為此使用函式 cv::warpAffine。
- 對變換後的影像應用旋轉。此旋轉是相對於影像中心的
- 等待使用者退出程式

本教程的程式碼如下所示。您也可以點選此處下載。

#include "opencv2/imgcodecs.hpp"

#include "opencv2/highgui.hpp"

#include "opencv2/imgproc.hpp"

#include <iostream>

using namespace cv;

using namespace std;

int main( int argc, char** argv )

{

CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );

Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );

if( src.empty() )

{

cout << "Could not open or find the image!\n" << endl;

cout << "Usage: " << argv[0] << " <Input image>" << endl;

return -1;

}

Point2f srcTri[3];

srcTri[0] = Point2f( 0.f, 0.f );

srcTri[1] = Point2f( src.cols - 1.f, 0.f );

srcTri[2] = Point2f( 0.f, src.rows - 1.f );

Point2f dstTri[3];

dstTri[0] = Point2f( 0.f, src.rows*0.33f );

dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );

dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

Mat warp_mat = getAffineTransform( srcTri, dstTri );

Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );

double angle = -50.0;

double scale = 0.6;

Mat rot_mat = getRotationMatrix2D( center, angle, scale );

Mat warp_rotate_dst;

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

imshow( "Source image", src );

imshow( "Warp", warp_dst );

imshow( "Warp + Rotate", warp_rotate_dst );

cv::Mat::empty

return 0;

}

bool empty() const
如果陣列沒有元素，則返回 true。
int64_t int64

cv::Mat
n 維密集陣列類
定義 mat.hpp:830

cv::Mat::size
MatSize size
定義 mat.hpp:2187

cv::Mat::cols
int cols
定義 mat.hpp:2165

定義 interface.h:61
cv::getTickFrequency
double getTickFrequency()

cv::Mat::rows
int rows
行和列的數量，如果矩陣維度超過2則為(-1, -1)
定義 mat.hpp:2165

cv::Mat::type
int type() const
返回矩陣元素的型別。

cv::Point_< float >

cv::String
std::string String
定義 cvstd.hpp:151

highgui.hpp

main
int main(int argc, char *argv[])
定義 highgui_qt.cpp:3

imgcodecs.hpp

imgproc.hpp

cv
定義 core.hpp:107

std
STL 名稱空間。

本教程的程式碼如下所示。您也可以點選此處下載。
from __future__ import print_function

import cv2 as cv

import numpy as np

import argparse

parser = argparse.ArgumentParser(description='Code for Affine Transformations tutorial.')

parser.add_argument('--input', help='Path to input image.', default='lena.jpg')

args = parser.parse_args()

src = cv.imread(cv.samples.findFile(args.input))

if src is None

print('Could not open or find the image:', args.input)

exit(0)

srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)

dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)

warp_mat = cv.getAffineTransform(srcTri, dstTri)

warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))

# 仿射變換後旋轉影像

center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)

angle = -50

scale = 0.6

rot_mat = cv.getRotationMatrix2D( center, angle, scale )

warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))

cv.imshow('Source image', src)

cv.imshow('Warp', warp_dst)

cv.imshow('Warp + Rotate', warp_rotate_dst)

cv.waitKey()

cv::samples::findFile
cv::String findFile(const cv::String &relative_path, bool required=true, bool silentMode=false)
嘗試查詢請求的資料檔案。

cv::imshow
void imshow(const String &winname, InputArray mat)
在指定視窗中顯示影像。

cv::waitKey
int waitKey(int delay=0)
等待按鍵按下。

cv::imread
CV_EXPORTS_W Mat imread(const String &filename, int flags=IMREAD_COLOR_BGR)
從檔案載入影像。

cv::warpAffine
void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar &borderValue=Scalar())
對影像應用仿射變換。

cv::getAffineTransform
Mat getAffineTransform(const Point2f src[], const Point2f dst[])
Calculates an affine transform from three pairs of the corresponding points.

cv::getRotationMatrix2D
Mat getRotationMatrix2D(Point2f center, double angle, double scale)
計算 2D 旋轉的仿射矩陣。
Definition imgproc.hpp:2591

解釋

載入影像

C++

CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );

Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );

if( src.empty() )

{

cout << "Could not open or find the image!\n" << endl;

cout << "Usage: " << argv[0] << " <Input image>" << endl;

return -1;

}

Java

String filename = args.length > 0 ? args[0] : "../data/lena.jpg";

Mat src = Imgcodecs.imread(filename);

if (src.empty()) {

System.err.println("Cannot read image: " + filename);

System.exit(0);

}

Python

parser = argparse.ArgumentParser(description='Code for Affine Transformations tutorial.')

parser.add_argument('--input', help='Path to input image.', default='lena.jpg')

args = parser.parse_args()

src = cv.imread(cv.samples.findFile(args.input))

if src is None

print('Could not open or find the image:', args.input)

exit(0)
仿射變換：如上所述，我們需要兩組3個點來推導仿射變換關係。請看

C++

Point2f srcTri[3];

srcTri[0] = Point2f( 0.f, 0.f );

srcTri[1] = Point2f( src.cols - 1.f, 0.f );

srcTri[2] = Point2f( 0.f, src.rows - 1.f );

Point2f dstTri[3];

dstTri[0] = Point2f( 0.f, src.rows*0.33f );

dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );

dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

Java

Point[] srcTri = new Point[3];

srcTri[0] = new Point( 0, 0 );

srcTri[1] = new Point( src.cols() - 1, 0 );

srcTri[2] = new Point( 0, src.rows() - 1 );

Point[] dstTri = new Point[3];

dstTri[0] = new Point( 0, src.rows()*0.33 );

dstTri[1] = new Point( src.cols()*0.85, src.rows()*0.25 );

dstTri[2] = new Point( src.cols()*0.15, src.rows()*0.7 );

Python

srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)

dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)

您可能想繪製這些點，以便更好地瞭解它們如何變化。它們的位置與示例圖（在理論部分）中所示的位置大致相同。您可能會注意到由3個點定義的三角形的大小和方向發生了變化。
有了這兩組點，我們使用OpenCV函式 cv::getAffineTransform 計算仿射變換。

C++

Mat warp_mat = getAffineTransform( srcTri, dstTri );

Java

Mat warpMat = Imgproc.getAffineTransform( new MatOfPoint2f(srcTri), new MatOfPoint2f(dstTri) );

Python

warp_mat = cv.getAffineTransform(srcTri, dstTri)

我們得到一個 \(2 \times 3\) 矩陣作為輸出（在本例中為 warp_mat）
然後我們將剛剛找到的仿射變換應用於源影像

C++

Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

Java

Mat warpDst = Mat.zeros( src.rows(), src.cols(), src.type() );

Imgproc.warpAffine( src, warpDst, warpMat, warpDst.size() );

Python

warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))

引數如下
- src: 輸入影像
- warp_dst: 輸出影像
- warp_mat: 仿射變換
- warp_dst.size(): 輸出影像的期望尺寸
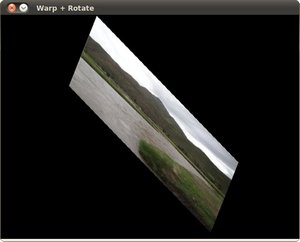
我們剛剛得到了第一張變換後的影像！我們將在一會兒顯示它。在此之前，我們還想旋轉它...
旋轉：要旋轉影像，我們需要知道兩件事
1. 影像將圍繞其旋轉的中心
2. 要旋轉的角度。在OpenCV中，正角度表示逆時針方向
3. 可選： 縮放因子
我們透過以下程式碼片段定義這些引數

C++

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );

double angle = -50.0;

double scale = 0.6;

Java

Point center = new Point(warpDst.cols() / 2, warpDst.rows() / 2);

double angle = -50.0;

double scale = 0.6;

Python

center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)

angle = -50

scale = 0.6
我們使用OpenCV函式 cv::getRotationMatrix2D 生成旋轉矩陣，它返回一個 \(2 \times 3\) 矩陣（在本例中為 rot_mat）

C++

Mat rot_mat = getRotationMatrix2D( center, angle, scale );

Java

Mat rotMat = Imgproc.getRotationMatrix2D( center, angle, scale );

Python

rot_mat = cv.getRotationMatrix2D( center, angle, scale )
現在我們將找到的旋轉應用於我們先前變換的輸出影像

C++

Mat warp_rotate_dst;

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

Java

Mat warpRotateDst = new Mat();

Imgproc.warpAffine( warpDst, warpRotateDst, rotMat, warpDst.size() );

Python

warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))
最後，我們會在兩個視窗中顯示結果，並額外顯示原始影像以作比較

C++

imshow( "Source image", src );

imshow( "Warp", warp_dst );

imshow( "Warp + Rotate", warp_rotate_dst );

Java

HighGui.imshow( "Source image", src );

HighGui.imshow( "Warp", warpDst );

HighGui.imshow( "Warp + Rotate", warpRotateDst );

Python

cv.imshow('Source image', src)

cv.imshow('Warp', warp_dst)

cv.imshow('Warp + Rotate', warp_rotate_dst)
我們只需等待使用者退出程式

C++

waitKey();

Java

HighGui.waitKey(0);

Python

cv.waitKey()

結果

編譯上述程式碼後，我們可以將影像路徑作為引數傳遞。例如，對於一張圖片，如下所示：

應用第一次仿射變換後，我們得到

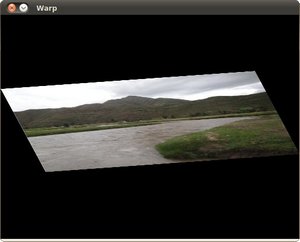
最後，在應用負旋轉（請記住負值表示順時針）和縮放因子後，我們得到


原始作者	Ana Huamán
相容性	OpenCV >= 3.0

目錄

目標

理論

什麼是仿射變換？

如何獲取仿射變換？

程式碼

解釋

結果